Let's pick a point $(x,y)$ on the parabola.
Then the vector $\mathbf d$ from $(X,Y)$ to $(x,y)$ is given by:
\[\mathbf d = \binom xy - \binom XY = \binom {x-X}{2x^2+4x+7/4-Y}\]
A tangential vector $\mathbf t$ at $(x,y)$ is the derivative:
\[\mathbf t = \d{}x \binom x{2x^2+4x+7/4}= \binom 1 {4x+4}\]
The corresponding line $p$ along $\mathbf d$ is normal if the dot product is zero:
\[\mathbf d \cdot \mathbf t = (x-X)+(2x^2+4x+7/4-Y)(4x+4) = 8x^3+24x^2+(24-4Y)x+(7-4Y-X) = 0\]
This is a cubic function, and according to
wiki, the critical distinction is when its discriminant $\Delta=0$, that is:
\begin{array}{}\Delta &=& 18abcd - 4b^3d + b^2c^2 - 4ac^3 - 27a^2d^2 \\
&= &18\cdot 8\cdot 24(24-4Y)(7-4Y-X)-4\cdot 24^3(7-4Y-X)+24^2(24-4Y)^2 \\
&& - 4\cdot 8 (24-4Y)^3-27\cdot 8^2(7-4Y-X)^2 \\
&=& -64(27X^2+54X-32Y^3+27) \\
&=& 0\end{array}
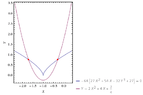
If we
plot this with Wolfram, we get:
View attachment 5933
In other words, we have 3 distinct normals if we are above that curve.
And we have 1 distinct normal if we are below that curve.
Oh, and the intersection points are at $\left(-1\pm\frac 1{\sqrt 2}, \frac 34\right)$, and the inverting point is at $(-1,0)$.