Finding expression for mass with tension, gravity and point charges

[wildredhead]

Homework Statement

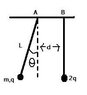
A small sphere carrying a charge of q with mass m is suspended from point A by a massless thread of length L, as shown in the figure. A second sphere carrying a charge of 2q with mass M is suspended from a fixed rod from point B. The distance between A and B is equal to d. At equilibrium the two spheres lie in the same horizontal plane and the thread makes an angle (theta) with the vertical.

a.) draw a free body diagram for the sphere suspended from point A.
b.) find an expression for the mass m in terms of q, L, theta, d ,g (gravitation acceleration), and k( Coulumb constant)
c. Find an espression for the tension T in the tread

Homework Equations

The Attempt at a Solution

My free body diagram consits of three forces: Fg pointing directly down from the sphere, Fe pointing directly left from the sphere. The problem doresn't have any negative charges so i figured they would be repeling therefore pointing left away from 2q. and I have Ft on L pointing upwards.

I have no idea how to approach the expression for mass. I was thinking that all the forces acting on the system would equal 0, but I don't know how to incorporate that into anything.

For c I did some searching online. So now I know the vertical component of tension to be equal to Fg. Fx then, would be equal to Fg(tangent(theta)) So Ft = Fg(tan(theta)) + Fg?

 

[rl.bhat]

Hi wildredhead, welcome to PF.
In the equilibrium position, what is the distance between the two charged spheres?
Once you know this distance, find the force of repulsion F on q.
Equate this force with one component of T. Equate the other component of T with mg.

 

[wildredhead]

Hi wildredhead, welcome to PF.
In the equilibrium position, what is the distance between the two charged spheres?
Once you know this distance, find the force of repulsion F on q.
Equate this force with one component of T. Equate the other component of T with mg.

the distance between the spheres would be something like the Lsin(theta) + d. Right? I use this in the Fe calculation... Fe= kq2q/Lsin(theta) +d. So I then use that as my x component for my tension force. Then the expression for mass is just g/F =M? I totally should have taken physics 2 right after physics 1 and not wait a semester.

 

[rl.bhat]

"kq2q/Lsin(theta) +d"
This should be
kq2q/(Lsin(theta) +d)^2
Next T*sinθ = Fe
T*cosθ = mg.
Now solve for m and T. Mass M does not come into picture.

 

[stickup]

Hey guys I have a similar problem to solve. I am stuck on the second part. I got the first part of the equation which is kq2q/lsin(thta) +d. Would we equal that to MG since F=MG? and then solve for M