- #1
Kizza23
- 1
- 0
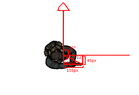
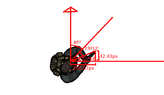
I am making a Scratch 3.0 game. The shooter sprite is holding a gun slightly off-centre (see images), and I need the bullet to go to the end of the barrel of the gun before traveling forward (as so it would appear the bullet it leaving the gun). The issue is, to do this, I need to find the X and Y distance of the end of the barrel from the centre of the shooter sprite (Scratch doesn't let you use diagonal distances 
). The X and Y distances change as the sprite rotates.
I know if the shooter sprite is facing 90º (right angle), the X distance to the gun is 105 pixels, and the Y distance is 45 pixels.
The computer always knows what direction the shooter sprite is facing.
What about the distances for all the other angles the shooter sprite is facing? Do I need a special formula?
View attachment 8942
View attachment 8943
). The X and Y distances change as the sprite rotates.I know if the shooter sprite is facing 90º (right angle), the X distance to the gun is 105 pixels, and the Y distance is 45 pixels.
The computer always knows what direction the shooter sprite is facing.
What about the distances for all the other angles the shooter sprite is facing? Do I need a special formula?
View attachment 8942
View attachment 8943
