goody1
- 16
- 0
Hello everyone, I need to find this limit
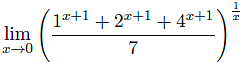 . What I tried is that
. What I tried is that
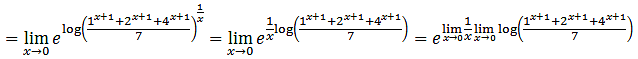 ,
,
but clearly, 1/x diverges so I don't think it was very helpful.
Could someone help me what I need to do please?
but clearly, 1/x diverges so I don't think it was very helpful.
Could someone help me what I need to do please?