Albert1
- 1,221
- 0
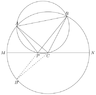
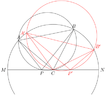
Points A,B are on circle C ,segment MN is a diameter of circle C, and point P is on
segment MN , if :
$\angle CAP=\angle CBP =10^o ,\,\, \overset{\frown} {MA}=40^o,\,\, find :\,\, \overset{\frown} {BN}=?$
segment MN , if :
$\angle CAP=\angle CBP =10^o ,\,\, \overset{\frown} {MA}=40^o,\,\, find :\,\, \overset{\frown} {BN}=?$
Last edited: