Finding possible heights of mercury in two joined manometers

[toforfiltum]

Homework Statement

[/B]

Homework Equations

ρ=hpg

The Attempt at a Solution

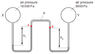
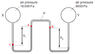
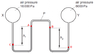
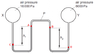
I really don't know how to rationalise the answer to this question. I just can't find the correct answer at all. The closest answer I thought was C and that too was also wrong since the pressure of mercury on the right side of manometer would be greater than 8000Pa in the right bulb. And the height difference among the two mercury column would add to the pressure of the left mercury column, making it greater than 13600Pa. So, I really am stuck at this question. Is my reasoning or concept wrong here, since I can't find the answer. By the way, the correct answer is D

 

[TSny]

Can you express the pressure at point A in terms of the pressure in bulb X and the height h₁? See figure below.

 

[toforfiltum]

Is it Ah₁= pressure in bulb X? Since point A is higher than point B

 

[TSny]

Is it Ah₁= pressure in bulb X?

What does "A" represent on the left hand side of this equation?

You should have studied a very fundamental formula that you can use to find the pressure difference between two points in a fluid at rest.

 

[TSny]

In your first post you wrote the equation ρ = hpg? Can you describe what each symbol stands for?

 

[toforfiltum]

Oh, sorry I don't think A represents anything, so is it just h₁=pressure in bulb X?

 

[TSny]

Oh, sorry I don't think A represents anything, so is it just h₁=pressure in bulb X?

No, h is a height. Height does not even have the same dimensions as pressure. So, writing h = pressure can't be correct.

 

[toforfiltum]

Oops,wrote the formula wrongly. Should be pressure=hρg, with h representing height, ρ for density and g for gravity

 

[toforfiltum]

So is h₁ρg=pressure in bulb X correct?

 

[TSny]

No, you need to think in terms of pressure differences. If h is the difference in height between two points a and b in a fluid at rest, then the pressure difference is P_b - P_a = ρgh where h is how much deeper b is compared to a.

How would this apply to the two points A and C shown below?

 

[toforfiltum]

Is the pressure difference between point A and C is h₁ρg?
Is the difference between point C and the other lowest point at bottom of bulb Y the pressure balancing pressure in bulb Y?

 

[TSny]

Is the pressure difference between point A and C is h₁ρg?

Yes. Make sure you understand which point is at the higher pressure. Can you write an equation that relates P_A, P_B, and h₁? [Edit: I meant to refer to points A and C, not A and B]

Is the difference between point C and the other lowest point at bottom of bulb Y the pressure balancing pressure in bulb Y?

Sorry, I don't understand what you are saying here. Can you write another equation that relates the pressures at points B and D in the figure below?

 

[toforfiltum]

Is it P_A-P_B=h₁ρg?

 

[TSny]

Oops, that was my fault. I meant to ask if you can write an equation that relates the pressures at points A and C (not A and B). Points A and C can be considered as two points in the same mercury fluid on the left.

 

[toforfiltum]

Is it P_A+h₁ρg= P_C?

 

[TSny]

Yes. Do you see that the pressure P_A is also the pressure, P, of the air in the middle horizontal section of the apparatus? Also, P_C is equal to the pressure in bulb X. So you can rewrite your equation by replacing P_A by P and P_C by P_X.

Now repeat this process for points B and D.

 

[toforfiltum]

Wow, I've got it. Thanks so much for pointing out the approach

 

[TSny]

Great! Good work!

 

[insightful]

Since 16000Pa = 12cmHG and 8000Pa = 6cmHg, what pressure P in the intermediate loop would give h1 = 18cm and h2 = 12cm?

 

[TSny]

Since 16000Pa = 12cmHG and 8000Pa = 6cmHg, what pressure P in the intermediate loop would give h1 = 18cm and h2 = 12cm?

Good point. I didn't bother to find P. To make it work I guess we could take the given pressures to be gauge pressures rather than absolute pressures.

 

[toforfiltum]

How to find P? I wonder how the P affects the pressure in this system.

 

[TSny]

How to find P? I wonder how the P affects the pressure in this system.

If (D) is the answer for the heights, then you can find P using your equation in post #15. P is the pressure at point A and the pressure in vessel X is the pressure at point C.

 

[toforfiltum]

Whys does the pressure turn out to be negative? Does it mean that part of the pressure from h₁ is supporting the pressure in bulb Y?

 

[TSny]

Absolute pressures cannot be negative. So, answer (D) cannot be correct if the pressures are absolute. If the pressures are gauge pressures, then (D) is a possible answer because it is OK to have negative gauge pressures as long as they are not less than -1 atm of pressure.