Calculate the manometer reading

[Bolter]

Homework Statement

See below

Relevant Equations

pressure = density * g * h

Having some trouble in answering part b) of this question

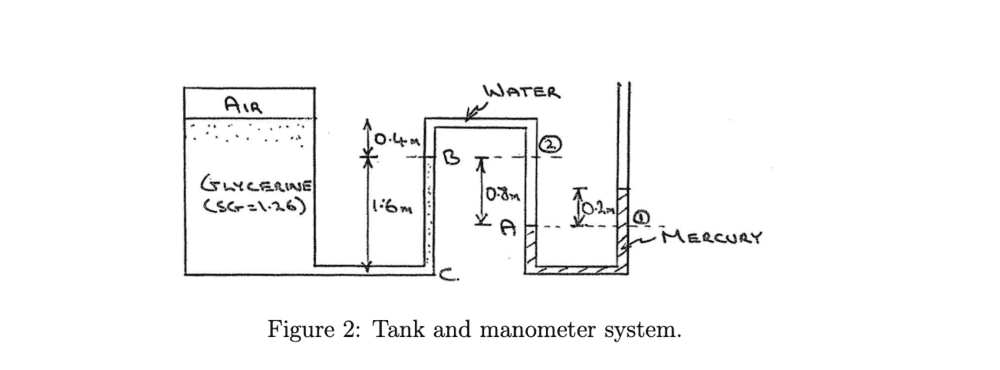
I managed to find the right answers for part a) if that is maybe needed in part b) which I got 26.7 kPa, 18.8 kPa, 38.6 kPa and 13.9 kPa for levels A, B, C and air pressure respectively

Not too sure what part b) is technically asking but I redrew the diagram and made the adjustment on the right side from what the question was asking

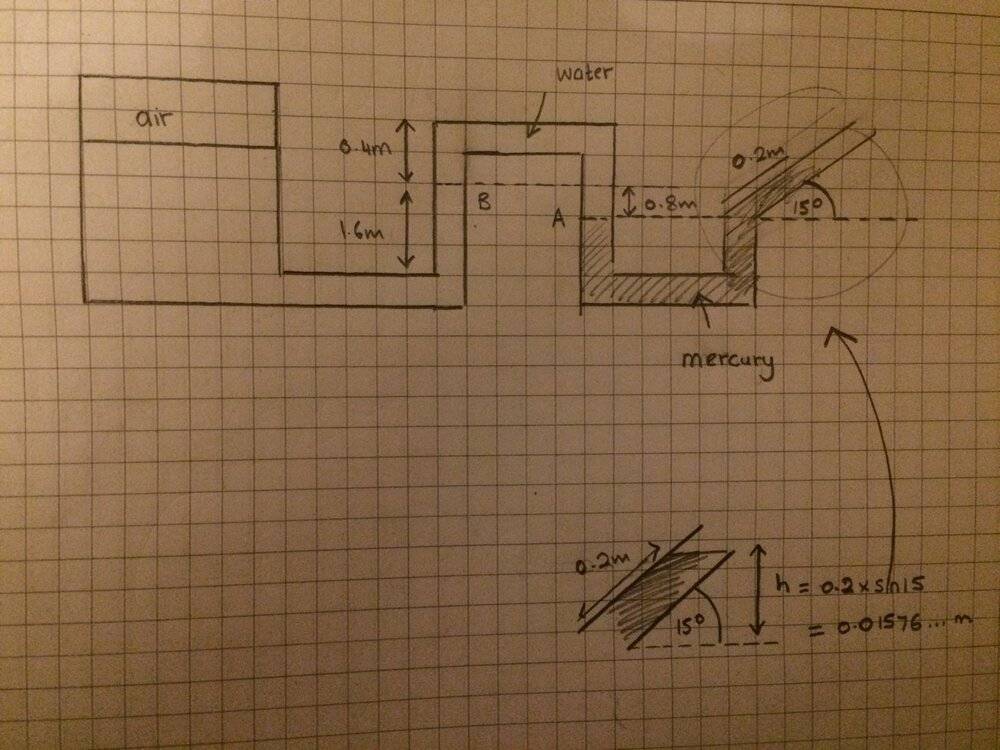
Would the new manometer reading be '0.2 x sin15 = 0.0576m as we're only concerned with the vertical change in height that affects pressure?

Any help would be appreciated! Thanks

 

[Lnewqban]

The level of the surface of mercury does not change because the pipe gets inclined, but it requires more mass inside the tube.
The inclination of one tube an its scale is common practice to be able to see very small variations of level, that would be difficult to spot in a vertical tube.
If you were not adding some mercury into the bent tube, you would be altering the balance previously achieved in a).

 

[Bolter]

The level of the surface of mercury does not change because the pipe gets inclined, but it requires more mass inside the tube.
The inclination of one tube an its scale is common practice to be able to see very small variations of level, that would be difficult to spot in a vertical tube.
If you were not adding some mercury into the bent tube, you would be altering the balance previously achieved in a).

I see. For the new manometer reading that it asks for, I only need to find the height difference between level A and new level of the surface of mercury. That gives me h = 0.2 * sin15 = 0.05176m = 51.76mm

But this is wrong as the correct answer is in fact 773mm which it says from the sheet.

 

[Lnewqban]

Perhaps if you consider 773 mm to be the hypotenuse of the triangle formed by height 200 mm and the angle?

Again, to keep balance of the system (same pressures and heights), the imaginary vertical column of mercury must remain being 200 mm.

 

[Bolter]

Perhaps if you consider 773 mm to be the hypotenuse of the triangle formed by height 200 mm and the angle?

Again, to keep balance of the system (same pressures and heights), the imaginary vertical column of mercury must remain being 200 mm.

Thanks I kept the imaginary vertical mercury column to remain as 200mm, and I managed to calculate 773mm in the end using basic trig. I got what the extra mercury mass needed to be too

 

[Lnewqban]

You are welcome