Finding probability of changing states

[TheCanadian]

I am following the derivation shown in this link on adiabatic passage.

I have posted one part below:

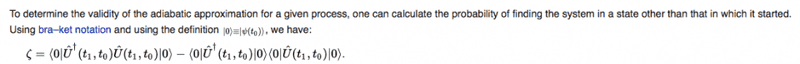
I am simply wondering how this expression was derived and how it indicates the probability of being in a state that is different from the initial state? How exactly is this represented by:

$$ \langle \hat{U}^\dagger(t_1,t_0)\hat{U}(t_1,t_0)\rangle - \langle \hat{U}^\dagger(t_1,t_0)\rangle\langle \hat{U}(t_1,t_0)\rangle $$

 

[Paul Colby]

The last term in your last expression is the probability that you will remain in the initial state. The first term is 1 by unitarity. The difference of these terms is the total probability of not being in the initial state.