Finding Side Lengths of Tangram Shapes

[Deeds]

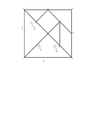
Hello, I'm trying to find the lengths of the sides of all of the shapes in the below tangram. This is what is given:
• 2 large, and congruent, isosceles right triangles
• 1 medium isosceles right triangle
• 2 small, and congruent, isosceles right triangles
• 1 square
• 1 parallelogram

The pieces can be rearranged with no gaps or overlapping of shapes into a square with dimensions 1 unit by 1 unit (i.e., the entire area of the square is 1 unit^{2}) You cannot make midpoint assumptions.

I've figured out the lengths of the two large triangles. (1 for the hypotenuse and \sqrt{2}/2 for the other two legs). Without assuming midpoints, I'm not sure where to go next. Thanks.

 

[johng1]

Hi,
I hope the following is understandable and helps.

 

[Deeds]

Hi,
I hope the following is understandable and helps.

Thank you so much for your help. Most of it I understand. I will sit with this later to see if I can get it to connect in my brain. :-) If not, I'll ask you more questions.

Again, thank you so much!

 

[Opalg]

See also http://mathhelpboards.com/geometry-11/tangrams-11357.html?highlight=tangram.

 

[Deeds]

Hi,
I hope the following is understandable and helps.

I'm confused about how you know that JF lies on a diagonal of the large square. I can understand how AK does and I can visually and conceptually see how JF would, but how can I mathematically show that?

Sorry, this problem is so difficult for me. Thanks again.

 

[Opalg]

I'm confused about how you know that JF lies on a diagonal of the large square. I can understand how AK does and I can visually and conceptually see how JF would, but how can I mathematically show that?

You know that AK is a diagonal of the large square. You also know that JF is perpendicular to AK (because the angles at F are right angles). Since the diagonals of a square are perpendicular to each other, it follows that JF must be parallel to the other diagonal. But since it passes through the vertex J, it must actually be part of that diagonal.