Finding the domain of a composite function

[member 731016]

Homework Statement

Pls see below

Relevant Equations

Pls see below

For this problem,

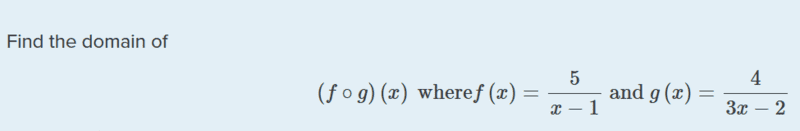
The solution is,

However, I tried solving this problem by using the definition of composite function

$f(g(x)) = f(\frac{4}{3x -2}) = \frac{5}{\frac{4}{3x - 2} - 1} = \frac{5}{\frac{6 - 3x}{3x - 2}} = \frac {15x - 10}{6 - 3x}$ which only gives a domain $x ≠ 2$. Would some please know how to find the solution from the composite function?

Many thanks!

 

[pasmith]

Consider: $$\frac{5}{\frac{4}{3x-2}-1} = \frac{5(3x-2)}{\left(\frac{4}{3x-2}-1\right)(3x-2)}.$$ This is fine if $x \neq 2/3$, but if $x = 2/3$ then multiplying numerator and denominator by $3x - 2$ is multiplying numerator and denominator by zero, which is not allowed.

 

[member 731016]

Consider: $$\frac{5}{\frac{4}{3x-2}-1} = \frac{5(3x-2)}{\left(\frac{4}{3x-2}-1\right)(3x-2)}.$$ This is fine if $x \neq 2/3$, but if $x = 2/3$ then multiplying numerator and denominator by $3x - 2$ is multiplying numerator and denominator by zero, which is not allowed.

Thank you for your reply @pasmith!

Sorry, why did you not multiply $\frac{4}{3x - 2}$ individually by the $\frac{3x-2}{3x-2}$?

Many thanks!

 

[Mark44]

Sorry, why did you not multiply $\frac{4}{3x - 2}$ individually by the $\frac{3x-2}{3x-2}$?

Here's from your work:

However, I tried solving this problem by using the definition of composite function $f(g(x)) = f(\frac{4}{3x -2})$

What do you get if x = 2/3 when you evaluate f(g(2/3))?

 

[SammyS]

Consider: $$\frac{5}{\frac{4}{3x-2}-1} = \frac{5(3x-2)}{\left(\frac{4}{3x-2}-1\right)(3x-2)}.$$ This is fine if $x \neq 2/3$, but if $x = 2/3$ then multiplying numerator and denominator by $3x - 2$ is multiplying numerator and denominator by zero, which is not allowed.

Thank you for your reply @pasmith!

Sorry, why did you not multiply $\frac{4}{3x - 2}$ individually by the $\frac{3x-2}{3x-2}$?

Many thanks!

Sure. If you distribute the $(3x-2)$ in the denominator and then simplify by "cancelling" and collecting terms, you will indeed get $\dfrac {15x - 10}{6 - 3x}$ which is $\dfrac {5(3x - 2)}{3(2 - x)}$ .

However, the point made by @pasmith is that the step he shows, which is required to get your final result;
that step is valid, only if $x\ne \dfrac 2 3$.

@Mark44 shows in a different way, why $x\ne \dfrac 2 3$.

If you study the given solution (the one you posted) seriously, you should notice that the first sentence there says much the same thing as Mark says.

 

[member 731016]

Here's from your work:

What do you get if x = 2/3 when you evaluate f(g(2/3))?

Thank you for your reply @Mark44!

I think I get undefined. However, I thought we were meant to simplify the composite function to that rational function in post #1 before substituting in values?

Many thanks!

 

[member 731016]

Sure. If you distribute the $(3x-2)$ in the denominator and then simplify by "cancelling" and collecting terms, you will indeed get $\dfrac {15x - 10}{6 - 3x}$ which is $\dfrac {5(3x - 2)}{3(2 - x)}$ .

However, the point made by @pasmith is that the step he shows, which is required to get your final result;
that step is valid, only if $x\ne \dfrac 2 3$.

@Mark44 shows in a different way, why $x\ne \dfrac 2 3$.

If you study the given solution (the one you posted) seriously, you should notice that the first sentence there says much the same thing as Mark says.

Thank you for your reply @SammyS!

I think I understand @pasmith method now! I guess it interesting that he did not simplify the fraction at first to see what values it was zero for, and then to find the other x-value you have to reduce it more to get the rational function I got. I guess this is interesting. Is there a way to remember this technique? I have not seen it in my calculus textbook.

With other composite function problems (without fractions) I have done, I just had to find the x-values that would not work for the final answer without having to do that in intermediate steps.

Many thanks!

 

[Mark44]

I think I get undefined. However, I thought we were meant to simplify the composite function to that rational function in post #1 before substituting in values?

No, not quite. You're asked to find the domain of f(g(x)), which means you have to find values of x for which g(x) is undefined, and values of g(x) for which f is undefined. These values will determine the domain of f(g(x)).

 

[SammyS]

With other composite function problems (without fractions) I have done, I just had to find the x-values that would not work for the final answer without having to do that in intermediate steps.

Well, for those problems, it looks like you were simply fortunate.

 

[member 731016]

No, not quite. You're asked to find the domain of f(g(x)), which means you have to find values of x for which g(x) is undefined, and values of g(x) for which f is undefined. These values will determine the domain of f(g(x)).

Thank you for your help @Mark44!

 

[member 731016]

Well, for those problems, it looks like you were simply fortunate.

Thank you for your help @SammyS! Oh ok, that's quite interesting because I solved quite a few of them using that method.

Many thanks!