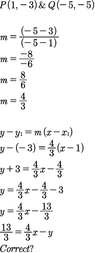Discussion Overview
The discussion revolves around finding the equation of a circle given the coordinates of its diameter endpoints, specifically points P(1, -3) and Q(-5, -5). Participants explore the mathematical steps necessary to derive the circle's equation in standard form, including determining the center and radius based on the given points.
Discussion Character
- Technical explanation
- Mathematical reasoning
- Debate/contested
Main Points Raised
- One participant suggests finding the radius by calculating the distance between points P and Q and dividing by 2, while also indicating the need to find the midpoint for the center of the circle.
- Another participant corrects the first by emphasizing that the midpoint is (3, 1) and calculates the radius as 2√10, based on the distance from the midpoint to either endpoint.
- Several participants reiterate the equation format as (x - h)² + (y - k)² = r², with h and k representing the center coordinates.
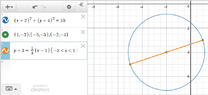
- One participant proposes an alternative equation, (x + 2)² + (y + 4)² = 10, claiming a different center and radius, which leads to further questioning of the midpoint and radius values.
- Another participant confirms the midpoint calculation as (-2, -4) and the radius as √10, providing a detailed derivation of these values and the resulting equation.
Areas of Agreement / Disagreement
Participants express disagreement regarding the correct midpoint and radius values, with some asserting that the midpoint is (3, 1) and others claiming it is (-2, -4). The discussion remains unresolved as multiple competing views persist regarding the correct equation of the circle.
Contextual Notes
There are limitations in the assumptions made about the midpoint and radius calculations, as well as the potential for misinterpretation of the endpoints' roles in determining the circle's properties. The discussion reflects differing interpretations of the mathematical steps involved.