Finding the Force Applied by a Support on a Falling Chain

[LCSphysicist]

Homework Statement

All below

Relevant Equations

All below

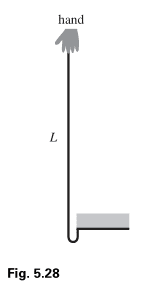
A chain with length L and mass density σ kg/m is held in the position
shown in Fig. 5.28, with one end attached to a support. Assume that
only a negligible length of the chain starts out below the support. The
chain is released. Find the force that the support applies to the chain, as
a function of time.

I am trying hard to see how the things work here. Try by conservation of energy is, to me, wrong.
I think the support's force need to stop the falling part and yet bear the weight of the fallen part.
To show my vision:

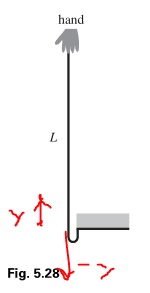this elementar mass at y fall actually twice y to come to rest.
It falls y in gt²2

So N = W + F = σyg + σv². But this seems wrong.

 

[etotheipi]

An idea; in a time $t$, the chain falls down a distance $\frac{1}{2}gt^2$. The two loops at the bottom each have a height of $\frac{1}{4}gt^2$.

If you can work out the centre of mass $\bar{y}$ of the whole chain in terms of $t$, then you can set $m\frac{d^2 \bar{y}}{dt^2}$ equal to the net external force on the whole chain .

 

[haruspex]

@etotheipi's approach is neat.
A more elementary way is to consider time t and a further interval dt. In dt, an element mass dm (you can express dm in terms of g, t, dt, and $\sigma$) comes to a halt from speed gt. What change of momentum does that represent?