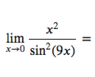ver_mathstats
- 258
- 21
- Homework Statement
- Find the limit as x approaches 0 x^2/(sin(^2)x(9x))
- Relevant Equations
- limit as x approaches 0 x^2/(sin(^2)x(9x))
Find the limit as x approaches 0 of x2/(sin2x(9x))
I thought I could break it up into:
limit as x approaches 0 ((x)(x))/((sinx)(sinx)(9x)).
So that I could get:
limx→0x/sinx ⋅ limx→0x/sinx ⋅ limx→01/9x.
I would then get 1 ⋅ 1 ⋅ 1/0. Meaning it would not exist.
However the solution is 1/81 in the textbook, would this mean I would have to multiply the numerator and denominator, specifically 1/9x by x/x to get x/9x2. If so, why would I have to do this? If this is wrong how would I approach this then?
Thank you.
I thought I could break it up into:
limit as x approaches 0 ((x)(x))/((sinx)(sinx)(9x)).
So that I could get:
limx→0x/sinx ⋅ limx→0x/sinx ⋅ limx→01/9x.
I would then get 1 ⋅ 1 ⋅ 1/0. Meaning it would not exist.
However the solution is 1/81 in the textbook, would this mean I would have to multiply the numerator and denominator, specifically 1/9x by x/x to get x/9x2. If so, why would I have to do this? If this is wrong how would I approach this then?
Thank you.