guyvsdcsniper
- 264
- 37
- Homework Statement
- Using your result from the previous part, and what you know about harmonic oscillators, find an expression for the allowed energies as a function of the quantum number n. Not that since we have two atoms, the mass that shows up in your calculations should be the reduced mass μ=1/(1/m1+1/m2)
- Relevant Equations
- U=1/2kx^2
Morse Potential
Taylor Series
E=(n+1/2)hbarw
This problem had me take the taylor series of the Morse Potential,
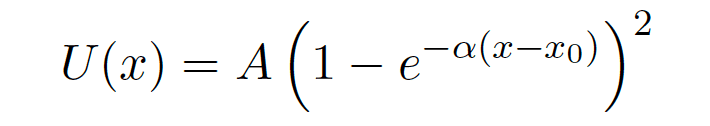
until I got the first non zero term.
My result was U(x)=Aα2(x-x0)2.
I know to find the quantum number I can use En=(n+1/2)ℏω and I know I can relate that to the potential energy of a harmonic oscillator, 1/2kx2. So if this taylor series is similar to the PE of a H.O. I can just substitute that.
The problem is my taylor series is off by a factor of 1/2, so it doesn't resemble the PE of a Harmonic Oscillator.
Can anyone help me see where I am going wrong.
EDIT:
I rechecked my work and I think I was incorrect. Forgot the the 1/2! for my first taylor expansion. My apologies for anyone who viewed this already. I have edited my post.

until I got the first non zero term.
My result was U(x)=Aα2(x-x0)2.
I know to find the quantum number I can use En=(n+1/2)ℏω and I know I can relate that to the potential energy of a harmonic oscillator, 1/2kx2. So if this taylor series is similar to the PE of a H.O. I can just substitute that.
The problem is my taylor series is off by a factor of 1/2, so it doesn't resemble the PE of a Harmonic Oscillator.
Can anyone help me see where I am going wrong.
EDIT:
I rechecked my work and I think I was incorrect. Forgot the the 1/2! for my first taylor expansion. My apologies for anyone who viewed this already. I have edited my post.
Last edited:
