lazypast
- 83
- 0
Homework Statement
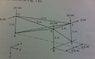
Hi. See attached, I need to determine the forces in all members.
Homework Equations
Sum of forces in X, Y & Z all equal 0.
Sum of moments in X, Y & Z all equal 0.
The Attempt at a Solution
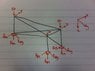
I've drawn the reactions at each support, A, B and C in my 2nd attached
ƩFx=0 ∴ 8+3-R(ax)-R(bx)-R(cx)=0
ƩFy=0 ∴ R(ay)+R(by)+R(cy)=0
ƩFz=0 ∴ 20+20+20-R(az)-R(bz)-R(cz)=0
After taking moments from various places and about various axis, I get Reactions at:
A-x= 8
y= 0
z=20
B-x= ?
y= 0
z= 9
C-x= ?
y= 0
z= 31
All in kN. The workings are just long winded so I'll put the important bit in - the unknowns R(bx) and R(cx).
Taking moments at A about the Z axis
0.866R(bx)+0.866R(cx)+0.866(3)+0.5R(cy)-0.5R(by)=0
R(cy)=R(by)=0 & dividing by 0.866
The equation becomes:
R(bx) + R(cx) = -3kN
I would say 3kN is shared equally between point C and B, but I have no proof, i.e. I can't see an equation that shows R(bx)=R(cx). Can I just assume 3kN is shared equally and R(bx) = R(cx) = 1.5kN