rugerts
- 153
- 11
Homework Statement
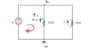
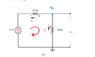
It's best if one looks at the picture of the circuit diagram. What we're given is a current of 0.25 A and two resistances of 20 and 30 ohms.
Homework Equations
Kirchhoff's Voltage Law, Kirchhoff's Current Law, Ohm's Law
The Attempt at a Solution
My attempt at a solution started with applying KVL to the first mesh (the leftmost) and I arrived at a value of 5V. Although I am a little confused as to the sign conventions here. I've read that it's best to follow passive sign convention, which from my understanding, says that current going into a resistor is labeled with a + polarity. Here, I go around the loop clockwise but arrive at a negative voltage value, which to me suggests the drawn arrow in the given diagram is going opposite to its true direction.
To find current 2, I tried applying KCL, which for me resulted in a value of current 2 being the same as current 1, which is not correct. Can anyone shed some light on why I must use Ohm's Law instead of KCL here to find current 2?
Attachments
Last edited by a moderator: