TheFallen018
- 52
- 0
Hey, I have this question I've been trying to figure out in an integration textbook. The part of the question that I'm having trouble understanding is basically this.
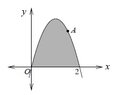
With the parabola below, find the x coordinate of A, if the line OA divides the shaded area into two equal parts.
View attachment 7519
The area of the parabola is 4 units^2.
The equation of the function is -3(x^2-2x))Would someone be so kind as to help me out with this one. I'm even quite sure how to approach this. Thanks.
With the parabola below, find the x coordinate of A, if the line OA divides the shaded area into two equal parts.
View attachment 7519
The area of the parabola is 4 units^2.
The equation of the function is -3(x^2-2x))Would someone be so kind as to help me out with this one. I'm even quite sure how to approach this. Thanks.