Khegan McLane's Math Problem: Rectangle Inscribed Between Parabola & X-Axis

[MarkFL]

Here is the question:

CAN SOMEONE HELP ME WITH THIS MATH PROBLEM?


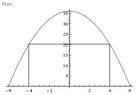
A rectangle is inscribed between the x-axis and the parabola y=36-x^3 with one side along the x- axis.

Part a.) Write the area of the rectangle as a function of x.

Part b) what values of x are in the domain of A

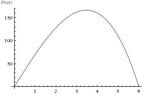
Part c) sketch a graph of A(x) over the domain.

Part d) Use your grapher to find the maximum area that such a rectangle can have.

any help would be nice.

I have posted a link there to this thread so the OP can see my work.

 

[MarkFL]

Hello Khegan McLane,

I assume you meant to give the parabola as $y=36-x^2$. Let's take a look at a rectangle so inscribed:

View attachment 1679

a.) The base of the rectangle is $2x$ and the height is $y=36-x^2$, hence the area $A$ of the rectangle is:

\(\displaystyle A(x)=2x\left(36-x^2 \right)=72x-2x^3\)

b.) In order for the height of the rectangle to be non-negative, we require:

\(\displaystyle -6\le x\le6\)

and in order for the base to be non-negative, we require:

\(\displaystyle 0\le x\)

Thus, in order to satisfy both conditions, we require:

\(\displaystyle 0\le x\le6\)

c.) Here is a plot of the area function on the relevant domain:

View attachment 1680

d.) Looking at the plot, it appears the maximum occurs when $x$ is a little more than 3.4. Using a bit of differential calculus, we can find the exact value.

Differentiating the area function with respect to $x$ and equating the result to zero, we obtain:

\(\displaystyle A'(x)=72-6x^2=6\left(12-x^2 \right)=0\)

The critical value in the domain is:

\(\displaystyle x=\sqrt{12}=2\sqrt{3}\)

The second derivative is:

\(\displaystyle A''(x)=-12x\)

Since our critical value is positive, the second derivative at that value is negative, demonstrating that this critical value is at a relative maximum. Thus, we conclude that the area of the rectangle is maximized for:

\(\displaystyle x=2\sqrt{3}\approx3.46410161514\)