Finding <x> using raising and lowering operators and orthonormality

[milkism]

Homework Statement

Finding P(x, t>0) and <x>.

Relevant Equations

See under.

I have this 1D LHO problem.

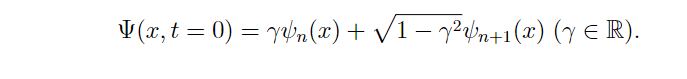
https://gyazo.com/4cd913d9da3a743443ef7dc2d1c2ab1e
For $\psi_n (x)$ I get
$$\left( \frac{\alpha}{\sqrt{\pi} 2^n n!} \right) ^{\frac{1}{2}} e^{\frac{- \alpha^2 x^2}{2}} H_n(x)$$
with $E_n = (n+ \frac{1}{2}) \hat{h} \omega$. where $\hat{h}$ is hbar.
For $\psi_{n+1}(x)$ I get
$$ \left( \frac{ \alpha }{ \sqrt{\pi} 2^{n+1} (n+1)!} \right) ^{\frac{1}{2}} e^{ \frac{- \alpha^2 x^2}{2}} H_{n+1}(x)$$
with $E_{n+1} = ((n+1)+ \frac{1}{2}) \hat{h} \omega$
We can find $\Psi(x,t>0)$ by multiplying the eigenfunctions with their corresponding factors and eigenenergies in the form of $\e^{-\frac{i}{\hat{h} E_n t}}$, to find $P(x, t>0)$ we basically take $|\Psi(x, t>0)|^2$ which I think will be a long expression.
But how can we find <x>, if we don't know the actual expressions for the Hermite polynomials? How can we compute the integral?

 

[milkism]

How come nothing got latexed :(

 

[erobz]

How come nothing got latexed :(

Use “$$”, not “$” for stand alone (centered) and for inline equations “##”.

 

[milkism]

Still doesn't work xd

 

[erobz]

Still doesn't work xd

You probably have an opened bracket somewhere.

 

[milkism]

Almost haha, I hope the unlatexed are understandable.

 

[erobz]

This one still is not quite right in your post:

$$ \left( \frac{ \alpha }{ \sqrt{\pi} 2^{n+1} (n+1)!} \right) ^{\frac{1}{2}} e^{ \frac{- \alpha^2 x^2}{2}} H_{n+1}(x)$$

As for the Physics... it's out of my league, but someone will be along.

 

[milkism]

Thanks!

 

[erobz]

Thanks!

you had some extra brackets in the exponent

 

[vela]

Use \hbar for $\hbar$.

Express $\hat x$ in terms of the raising and lowering operators and use the orthogonality of the energy eigenstates.

 

[milkism]

Use \hbar for $\hbar$.

Express $\hat x$ in terms of the raising and lowering operators and use the orthogonality of the energy eigenstates.

Do I have to change the x in the $$\psi(x)$$ terms also in terms of raising-ladder operators? Or only $\hat{x}$ in $$< \Psi | \hat{x} | \Psi >$$

 

[milkism]

Also I can't write anyting right now so I am using my head, don't we need to use two orthogonality expressions? One for $\psi (x)$ and one for the Hermite polynomials? Which do not have the same form of orthogonality. And also norm for Hermite squared is different. So I first solve the integral w.r.t x for $\psi (x)$ then an another integral for the hermites w.r.t alpha x?

 

[milkism]

Nevermind, I'm lost, I don't know how can I use orthogonality in finding expectation value of x, if it was taking integral of probability, no problem.

 

[milkism]

Oh! Wait I can rewrite x as $$\frac{\chi}{\alpha}$$ then my integral will look something like

 

[vela]

Also I can't write anyting right now so I am using my head, don't we need to use two orthogonality expressions? One for $\psi (x)$ and one for the Hermite polynomials? Which do not have the same form of orthogonality.

The orthogonality of the wave functions is the same as the orthogonality of the Hermite polynomials. You're probably confused because your expression for the wave function is slightly incorrect. $H(x)$ should be $H(\alpha x)$. The argument of the Hermite polynomial should be dimensionless, so it can't just be a plain $x$ which has dimensions of length.

 

[milkism]

Oh! Wait I can rewrite x as $$\frac{\chi}{\alpha}$$ then my integral will look something like
View attachment 337863

Oh wait nevermind we would get $$e^\frac{-\chi ^4}{4}$$

 

[milkism]

OMG am so dumb, i forgot exponent rules!

 

[milkism]

Is the solution
$$ < x > = \frac{1}{\alpha} \left( \gamma ^2 \left( \frac{\alpha}{\sqrt{\pi}2^n n!} \right) + (1- \gamma^2) \left( \frac{\alpha}{\sqrt{\pi}2^{n+1} (n+1)!} \right) \right)$$?

 

[vela]

No, your expression should have units of length. The factors of $\alpha$ cancel out, so your expression is unitless. Also, normalization should get rid of many of the constants you still have there.

 

[milkism]

Oh! Wait I can rewrite x as $$\frac{\chi}{\alpha}$$ then my integral will look something like
View attachment 337863

Oh, nevermind I misread this formula I thought there was an extra $\chi$ there

 

[milkism]

Do I literally have to integrate the four terms that there will be? I am lost.

 

[milkism]

i guess this is the formula, am unsure how to find the coefficients c_i tho.

 

[milkism]

Is it
$$2 \gamma \sqrt{1-\gamma ^2} \sqrt{\frac{\hbar}{2m \omega}} cos(\omega t)$$?
@vela

 

[vela]

Please show your work.

 

[kuruman]

Do I literally have to integrate the four terms that there will be? I am lost.

You can find the needed integrals without doing any integration if you use the raising and lowering opertors as suggested by @vela.

First write down what you get when they operate on the eigenstates $\psi_n$
$a_{+}\psi_n=~?$ $~~~a_{-}\psi_n=~?$

Second, noting that $~~\hat x=\sqrt{\dfrac{\hbar}{2m\omega}}(a_{+}+a_{-})$, find $~~\hat x \left(\gamma~ \psi_n+\sqrt{1-\gamma^2}~\psi_{n+1}\right)=~?$ You should get a linear combination of four eigenstates.

Third, find $$\int\left(\gamma~ \psi^*_n+\sqrt{1-\gamma^2}~\psi^*_{n+1}\right)\left[\hat x \left(\gamma~ \psi_n+\sqrt{1-\gamma^2}~\psi_{n+1}\right)\right]dx=~?$$ Do NOT integrate explicitly. Use the orthonormality condition $\int \psi^*_i\psi_j dx=\delta_{ij}$ to find the answer.

Show your work!