Fluid Mechanics: Hydrostatic Pressure on a gate with hinges

[Feodalherren]

Homework Statement

Homework Equations

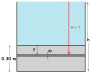
Fluid Mechanics

The Attempt at a Solution

Lets start with the easy part:

The pressure of the air is constant so the pressure will act as if it's a concentrated force on the center of gravity of the gate.

F = PA = (10,000Pa)(.3)(.6)=1800N

The moment about B = 1800N (.15m) = 270Nm.

Now we know that the water has to exert a 270Nm torque to make the gate move.

This is where I'm stuck. I'm not sure how to find the torque that the water exerts on the gate. Depending on the ratio of h to the height of the door, .3, it seems to me that the concentrated force of the water might land above the door. So it seems to me like I can't use the same method. I feel like I need to integrate and add up all the small moments across the whole door.

So the integral would be something like

integrating from B to .3

M = ∫ γ(volume of water)dy

but I don't know anything else except the height for the water...

 

[TSny]

I feel like I need to integrate and add up all the small moments across the whole door.

So the integral would be something like

integrating from B to .3

M = ∫ γ(volume of water)dy

but I don't know anything else except the height for the water...

OK. You have the right idea. If you let y denote depth below point B, how would you express the force from the water on a horizontal strip of the gate if the strip extends from y to y+dy?

 

[Feodalherren]

Hmm I'm not sure. I guess that's kind of where I'm stuck.

The pressure would depend on h and I'm not sure how to relate h to the length of the gate.

 

[TSny]

From the picture below, what is the depth, H, of the strip below the surface of the water in terms of h, y, and .30 m?

 

[Feodalherren]

H= h + y - .30

?

 

[TSny]

H= h + y - .30

?

Yes. So, you can express the force on the strip in terms of H, and therefore in terms of y and h.

 

[Feodalherren]

Ok so dA= .6 dy

The force exerted by the water on a differential of the area is

Fw = P(.6)dy

The pressure of the water:

ϒ = 9790 N / m^3

P= ϒ(h+y-.3)

then the force becomes (ignoring direction since we know it's opposite to the direction of the force of the air).

Fw(total) = ∫ ϒ(h+y-.3)(.6)dy

integrate from 0 to .3

is that correct?

 

[TSny]

The pressure of the water:

ϒ = 9790 N / m^3

P= ϒ(h+y-.3)

OK, I guess you're using 9.79 m/s² for g.

then the force becomes (ignoring direction since we know it's opposite to the direction of the force of the air).

Fw(total) = ∫ ϒ(h+y-.3)(.6)dy

integrate from 0 to .3

is that correct?

This would yield the force, but you want the torque.

 

[Feodalherren]

The number came out of my book, Fluid Mechanics by Frank White 5th ed.

Yeah I just wanted to check my logic. Okay so if that's the total force then the total torque must just be the total force multiplied by the distance

T = F y

where y is the distance from B to the point of application of the force.

so

T = ∫ ϒ(h+y-.3)(.6)y dy

correct?

 

[TSny]

Looks good.

 

[Feodalherren]

Thank you so much! I got the correct answer!

 

[TSny]

Great! Good work.