Focal length calculation and graph Q

[_Greg_]

Hi folks, just joined the forums
Hope you don't mind me firing a few questions now and again, i have some reports to do over the weekend which is the last of my HNC in Chemical Engineering :!)
A lot of it is basic physics which iv done in the past but its just the odd bit that catches me out.

So anyway, iv done an expeiment with a converging lens where you alter the object distance and image distance ( U & V ) to get focused images on the screen.
With these results iv plotted a graph of V against U which produces a curved slope (diagram 1)

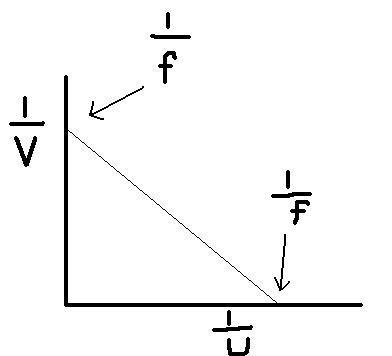
Then i done a graph of 1/V and 1/U which produces a straight line which intercepts the x and y axis, these values being 1/f (diagram 2)

My question is

Why is the graph of U and V not useful for finding the focal length of the lens accurately?

probably an easy question but i just can't put my finger on it :shy:

cheers

 

[esalihm]

use similar triangles to proove that the formula for a lens is (1/U + 1/V = 1/f)
or u can find it anywhere on the internet. it is a very easy proof, won't take you 5 min.

therefore it is 1/U and 1/V not U and V

 

[_Greg_]

not entirly sure what you mean, triangles?
anyway, that 1/V vs 1/U graph with my experimental results is proof that the equation is true.
im just asked why the U and V graph doesn't give an accurate value for the focal length?

 

[esalihm]

ok

if you draw your object, lens and image on a piece of paper with two of the rays you use to draw a ray diagram, you can see that there are some similar triangles on that figure. Try using similar triangles and getting two equations involving U, V and f.

then solve them simultaneously to get "1/U + 1/V = 1/f "

(if you cannot I can give you the solution but try it first :)

U and V graph cannot give you an accurate value for the focal length because the relation between the two is not related to f in any simple way.
if u play around with the equation I gave you above you might get " "[(v+U)/U]*f=V" but this won't make it any easier.

perhaps the answer to your question is that the nature of lenses does not provide us with that simple relations where you plot U versus V and get a slope or a y intercept of f