DonLumpo
- 1
- 0
Summary: How to explain the focusing properties of a 2D parabolic mirror based on third-order aberration theory?
Hello everyone,
I am currently studying with full-wave simulations the focusing properties of a 2D parabolic mirror, i.e. the scattered fields resulting from plane wave incidence at oblique angles.
What I observe for shallow reflectors is that the maxima of the scattered field generally lie on a curve that bends towards the reflector for increasing angles of incidence, just as the tangential focal surface shown in the attached figure.
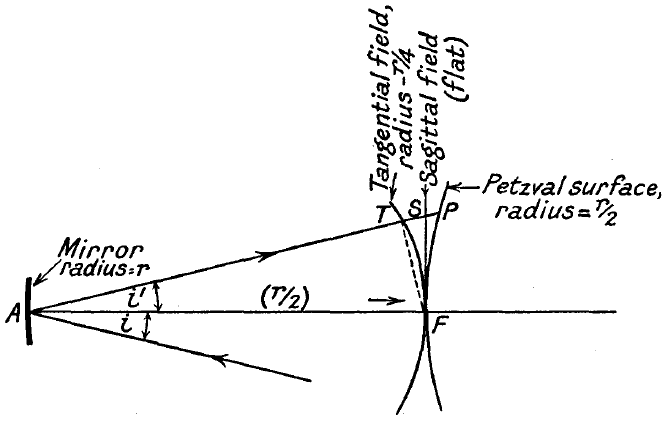
What I learned for the 3D case (paraboloid mirror) is the following:
- As every optical system, the mirror has associated with it a sort of basic field curvature, called the Petzval curvature. When there is no astigmatism, the sagittal and tangential image surfaces coincide with each other and lie on the Petzval surface
- The sagittal focal surface from third-order Seidel aberration theory is the focal plane, and the tangential focal surface lies between the focal plane and the mirror
- As in any optical system, the tangential surface is three times as far from the Petzval surface as the sagittal surface
Now my question is, how can the focusing contour that I observe for the 2D case (obviously astigmatism is not defined in 2D) be explained with this/third-order aberration theory?
Many thanks
Hello everyone,
I am currently studying with full-wave simulations the focusing properties of a 2D parabolic mirror, i.e. the scattered fields resulting from plane wave incidence at oblique angles.
What I observe for shallow reflectors is that the maxima of the scattered field generally lie on a curve that bends towards the reflector for increasing angles of incidence, just as the tangential focal surface shown in the attached figure.
What I learned for the 3D case (paraboloid mirror) is the following:
- As every optical system, the mirror has associated with it a sort of basic field curvature, called the Petzval curvature. When there is no astigmatism, the sagittal and tangential image surfaces coincide with each other and lie on the Petzval surface
- The sagittal focal surface from third-order Seidel aberration theory is the focal plane, and the tangential focal surface lies between the focal plane and the mirror
- As in any optical system, the tangential surface is three times as far from the Petzval surface as the sagittal surface
Now my question is, how can the focusing contour that I observe for the 2D case (obviously astigmatism is not defined in 2D) be explained with this/third-order aberration theory?
Many thanks
Last edited: