- #1
StephenDoty
- 265
- 0
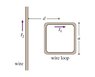
A square loop of wire with side length, a, carries a current I_1. The center of the loop is located a distance d from an infinite wire carrying a current I_2. The infinite wire and loop are in the same plane; two sides of the square loop are parallel to the wire and two are perpendicular as shown. What is the magnitude, F, of the net force on the loop? (See picture below)
Now I know that F= IL X B
and the force of two wires is F= (u0 * L * I1 * I2)/(2*pi*d)
but I am at a loss as to how to start this problem.
Please help.
Thanks.
Stephen
Now I know that F= IL X B
and the force of two wires is F= (u0 * L * I1 * I2)/(2*pi*d)
but I am at a loss as to how to start this problem.
Please help.
Thanks.
Stephen