- #1
Badger
- 28
- 0
Hello all, I thought I was starting to understand these magnetic field problems but this one is driving me crazy. I've inputted a good 6 or 7 answers and they all failed. Help would be awesome as always.
A square loop of wire with side length a carries a current I_1. The center of the loop is located a distance d from an infinite wire carrying a current I_2. The infinite wire and loop are in the same plane; two sides of the square loop are parallel to the wire and two are perpendicular as shown.
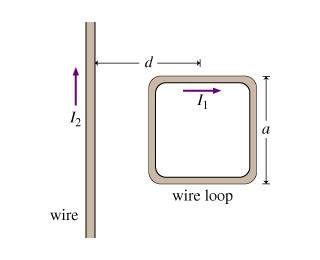
What is the magnitude, F, of the net force on the loop?
Express the force in terms of [tex]I_1, I_2, a, d, mu_0[/tex]
None are given, but my guess is this guy will be involved:
F_parallel_wire = I_x L B_y ; x is one wire, y is another wire
F_p_w = (u_0 * L * I_1 * I_2) / 2(pi)d
Ampere's Law as well:
circle integeral of B * ds = BL = B(2(pi)d = u_0 * I_through
Most recent answer.
just to make this easier, mu_0 = u and pi = p
F = I L B
F = I_1 * [(d+.5a) + (d-.5a)] * [(u * I_2)/(2 * p * a)]
not right.
So anyway, there's 4 sides to the loop so there should be 4 forces.
F_top_loop is equal and opposite to F_bottom_loop so those can be tossed aside.
F_left has the same direction of current as the wire so they attract. Negative sign.
F_right has the opposite direction of current as wire so they repel. Positive sign.
F_left than F_right to the wire so it'll have a stronger force and the direction will go left.
The distance between the closer ones is d - .5a and the distance between the distant ones is d + .5a
B = u_0(I_2)/(2(pi)d)
since the length of the wire isn't provided, I figure d will be the amount in parallel with the part of the loop, in this case a. d = a.
Homework Statement
A square loop of wire with side length a carries a current I_1. The center of the loop is located a distance d from an infinite wire carrying a current I_2. The infinite wire and loop are in the same plane; two sides of the square loop are parallel to the wire and two are perpendicular as shown.
What is the magnitude, F, of the net force on the loop?
Express the force in terms of [tex]I_1, I_2, a, d, mu_0[/tex]
Homework Equations
None are given, but my guess is this guy will be involved:
F_parallel_wire = I_x L B_y ; x is one wire, y is another wire
F_p_w = (u_0 * L * I_1 * I_2) / 2(pi)d
Ampere's Law as well:
circle integeral of B * ds = BL = B(2(pi)d = u_0 * I_through
The Attempt at a Solution
Most recent answer.
just to make this easier, mu_0 = u and pi = p
F = I L B
F = I_1 * [(d+.5a) + (d-.5a)] * [(u * I_2)/(2 * p * a)]
not right.
So anyway, there's 4 sides to the loop so there should be 4 forces.
F_top_loop is equal and opposite to F_bottom_loop so those can be tossed aside.
F_left has the same direction of current as the wire so they attract. Negative sign.
F_right has the opposite direction of current as wire so they repel. Positive sign.
F_left than F_right to the wire so it'll have a stronger force and the direction will go left.
The distance between the closer ones is d - .5a and the distance between the distant ones is d + .5a
B = u_0(I_2)/(2(pi)d)
since the length of the wire isn't provided, I figure d will be the amount in parallel with the part of the loop, in this case a. d = a.