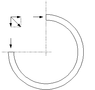
SUMMARY
The discussion centers on calculating the net force exerted by a liquid of density ρ flowing through a tube bent into a three-quarter circular arc of radius R. The relevant equation identified is F = ρAv², where A is the cross-sectional area and v is the linear speed of the liquid. The net force results from the action/reaction pairs at the tube's input and output, leading to a resultant force of √2 * ρAv² when considering the vector addition of forces at right angles. The conversation emphasizes the importance of understanding centripetal acceleration and the dynamics of fluid flow within the tube.
PREREQUISITES
- Understanding of fluid dynamics principles
- Familiarity with centripetal acceleration concepts
- Knowledge of vector addition in physics
- Basic proficiency in applying the equation of motion for fluids
NEXT STEPS
- Study the derivation of centripetal acceleration in fluid systems
- Learn about vector addition and its application in physics
- Explore the implications of Bernoulli's principle in fluid dynamics
- Investigate the effects of varying cross-sectional areas on fluid flow
USEFUL FOR
Students in physics or engineering disciplines, particularly those focusing on fluid dynamics, mechanical engineers, and anyone involved in designing systems that utilize fluid flow through curved tubes.