Force on rectangular loop by a current in a long straight wire

[cherry]

Homework Statement

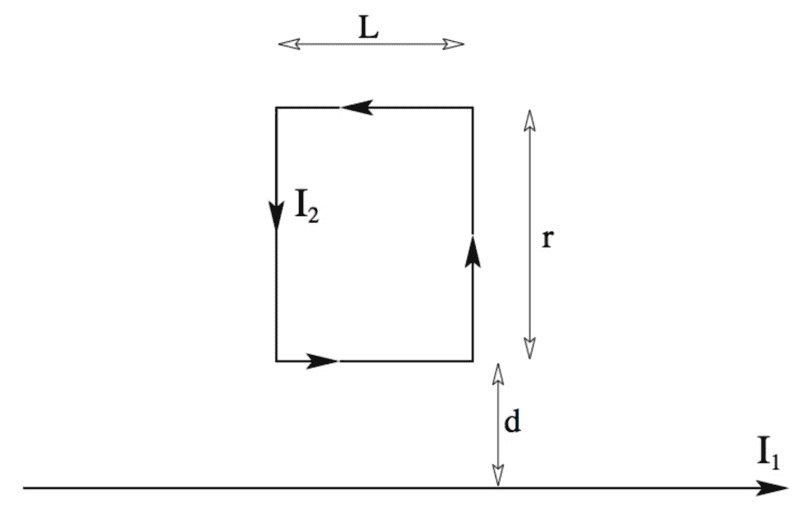
Consider a long straight wire near a rectangular loop of wire as shown below. The bottom of the rectangle is a distance d = 5.0 cm from the straight wire at its nearest approach, with length L = 16.0 cm and width r = 9.0 cm (so the far edge is at distance d+r from the straight wire).

When I1 = 100.0A and I2 = 40.0A, each in the direction indicated with the arrows, what is the net force on the rectangle of wire?

Relevant Equations

B = μI/2πd
F = Il x B

Hi, I am struggling to get the right answer for this question.

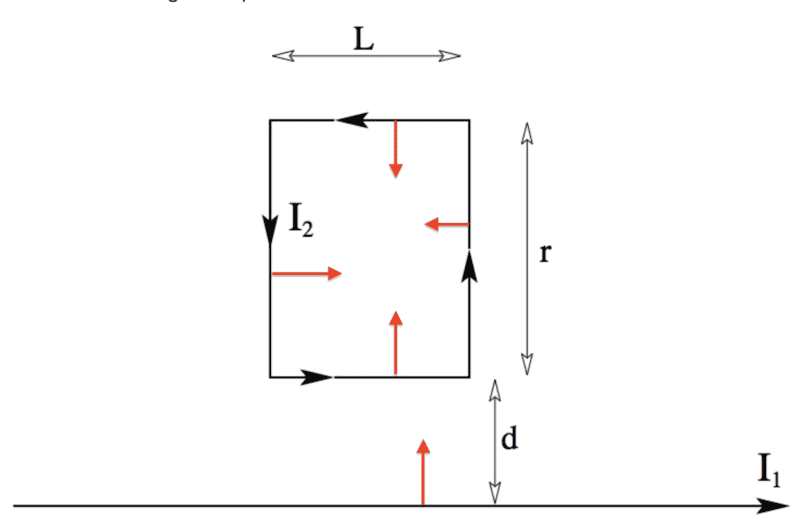
My first thought was that I should consider to what direction does each segment of wire have a force towards.
I found the direction to be in the following (see red arrows):

My past attempt was:
F_loop = I_loopl_loopB_wire
Since B_wire = μ_o I_wire / 2πd
= 2 * 10^-7 * 40 * 0.16 * 100 / 0.05
= 2.56 x 10^-3

What I am confused is first of all, is that the force on the rectangular loop is DOWN and not UP (I got this from a multiple choice question that asked for the direction of the force on the rectangular loop).

Am I missing something in this question?
Do I have to solve by calculating the force on each loop segment (ex: solve for top, bottom, left, and right)?

Thank you!

 

[BvU]

Hi,
You have me wondering what you are calculating, why and especially: how ?

The exercise asks for the force on the loop. So you need B wire, but is that a single value ?

Also, I wonder about the red arrows...

 

[cherry]

Hi,
You have me wondering what you are calculating, why and especially: how ?

The exercise asks for the force on the loop. So you need B wire, but is that a single value ?

Also, I wonder about the red arrows...

My understanding of the question was that since current is a single value, the magnetic field is uniform across the wire and the rectangular loop. Hence, why B wire is also a single value.

I got the direction of force using the RHR.

 

[kuruman]

Do I have to solve by calculating the force on each loop segment (ex: solve for top, bottom, left, and right)?

Yes, but you need to get the directions of the forces correctly. Note that segments on opposite sides of the loop carry antiparallel currents. Do antiparallel currents attract or repel?

 

[haruspex]

Do I have to solve by calculating the force on each loop segment (ex: solve for top, bottom, left, and right)?

Yes, because this is wrong:

My understanding of the question was that since current is a single value, the magnetic field is uniform across the wire and the rectangular loop. Hence, why B wire is also a single value.

To find the field from the wire at the loop you divided by d, but that only gives the field at the nearest part of the loop. It will be less elsewhere.