A13235378
- 50
- 10
- Homework Statement
- A plate is in the shape of a quarter cylinder of radius R and length L. This plate is hinged at C to a vertical wall and can rotate freely about C. The end A of the plate is tied to the wall using two horizontal cables the other cables is parallel to OA and the two cables are placed symmetrically). the space between the wall and the plate is filled completely with water (density=rho) Neglect the weight of the plate and calculate the tension in each cable .
- Relevant Equations
- p = rho . g . h (pression)
Before, sorry for my English, it is not my native language
I already have the solution to the issue, I just didn't understand a step.
1) Calculation of weight force (vertical):
$$ F_v = \frac{\rho \pi R^2 . L .g}{4}$$
2) Calculation of force due to water pressure on the plate (horizontal)
Mean pressure . effective area = $$ \frac{\rho . g . R}{2} . RL = \frac {\rho g R^2 .g} {2} $$
From this, the resulting force between the two forces is calculated and its direction must pass through point O.
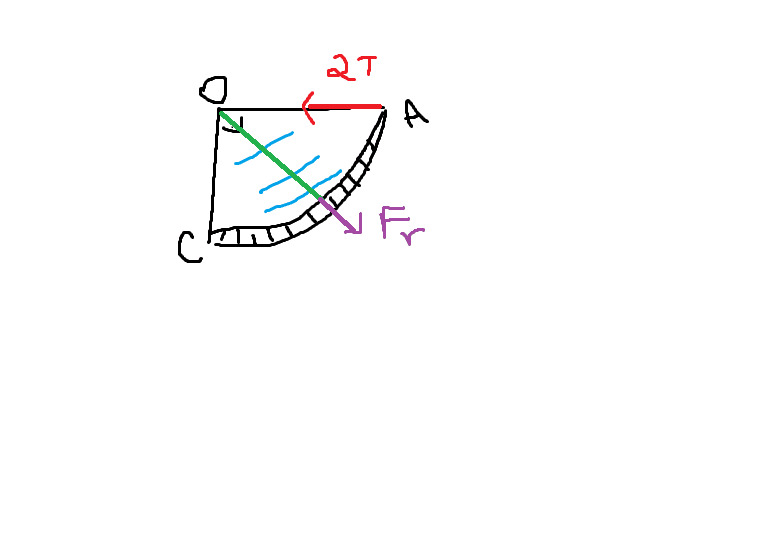
My doubt is exactly this: why do you need to go through the O point?
I already have the solution to the issue, I just didn't understand a step.
1) Calculation of weight force (vertical):
$$ F_v = \frac{\rho \pi R^2 . L .g}{4}$$
2) Calculation of force due to water pressure on the plate (horizontal)
Mean pressure . effective area = $$ \frac{\rho . g . R}{2} . RL = \frac {\rho g R^2 .g} {2} $$
From this, the resulting force between the two forces is calculated and its direction must pass through point O.
My doubt is exactly this: why do you need to go through the O point?