SUMMARY
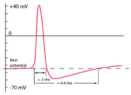
This discussion focuses on creating a precise formula for modeling the action potential of a neuron, specifically using the Hodgkin-Huxley model. Participants suggest various mathematical approaches, including the use of exponential functions and piecewise continuous functions, to approximate the action potential curve. The goal is to graph this model in the Desmos graphics calculator while ensuring accuracy in key voltage values, such as -70 mV for resting potential and +40 mV for peak action potential. A numerical solution is recommended for better precision, as Desmos cannot solve differential equations directly.
PREREQUISITES
- Understanding of the Hodgkin-Huxley model for action potentials
- Familiarity with exponential functions and their applications
- Basic knowledge of differential equations and numerical methods
- Experience with graphing tools like Desmos
NEXT STEPS
- Explore numerical integration techniques for solving differential equations
- Learn about piecewise functions and their applications in curve fitting
- Investigate the use of the Hodgkin-Huxley model in computational biology
- Research audio sonification techniques for representing mathematical functions
USEFUL FOR
Researchers in computational biology, educators developing resources for visually impaired learners, and anyone interested in mathematical modeling of biological systems.