How to graph the duffing frequency response

[Takuza]

I`ve been able to use excel to plot the trajectory of a harmonically driven duffing oscillator for arbitrary parameters using Runge-Kutta method. I would like to do the same thing for the frequency response, but I simply can not figure out how. I am not very mathematically advanced so the first thing I did was look for a formula. I found things such as those in the attached images, where A is the amplitude which I would like to plot as a function of w (frequency) (and all other terms are knowns). But I have no idea how to make use of these equations. I don't know how to isolate the amplitude and don`t know how to graph it without isolating A.

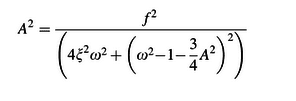
Can someone explain to me how one would plot the frequency response to a duffing oscillator ? It must be obvious, as every book I`ve read skips right over it as if it deserves no explicit explanation, but I am at a loss and have been trying for a while. Sorry if this is a dumb issue, I have no background in this area

Edit: I`ve also attached the VBA code I`m using in case that provides some insight somehow

 

[S.G. Janssens]

I`ve been able to use excel to plot the trajectory of a harmonically driven duffing oscillator for arbitrary parameters using Runge-Kutta method. I would like to do the same thing for the frequency response, but I simply can not figure out how.

For arbitrary parameters, you will not be able to obtain a frequency response. It only makes sense in the weakly forced regime, see the section titled "The weakly forced system: nonlinear resonance" here:

http://www.scholarpedia.org/article/Duffing_oscillator

You may find it interesting to look at the curves in Figure 6. As you can see, their derivation is not straightforward, in the sense that it is based on a technique called "averaging".

The graph of the coordinates of the equilibria of the averaged system as a function of the angular driving frequency shows implicit curves. In other words, it will not be possible to obtain explicit expressions as a function of $\omega$. You can use any software that can do implicit plotting (such as MATLAB) to reproduce them. Free packages written specifically for this purpose are MATCONT and AUTO, although the first one requires MATLAB.