Fourier Series of Even Square Wave

[sandy.bridge]

Homework Statement

$-0.5\leq{t}\leq{1.5}, T=2$
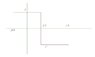
The wave is the attached picture.

I need to determine the Fourier Series of the wave in the picture.

I know that $$f(t)=a_0+{\sum}_{n=1}^{\infty}a_ncos(n\omega_0t)+{\sum}_{n=1}^{\infty}b_nsin(n\omega_0t)$$

where $a_0=\bar{f}=0$ due to being an even function. Furthermore, $b_n=0$ due to being an even function also.

That leaves,
$$a_n=\int_{-0.5}^{0.5}cos(n\omega_0t)dt-\int_{0.5}^{1.5}cos(n{\omega}_0t)dt=0-\frac{1}{n\omega_0}(sin(1.5n{\omega}_0t)-sin(0.5n{\omega}_0t))=\frac{1}{n{\omega}_0}(sin(0.5n{\omega}_0t)-sin(1.5n{\omega}_0t))$$

therefore,
$$f(t)=\frac{1}{{\omega}_0}\sum_{n=1}^{\infty}cos(n{\omega}_0t)(sin(0.5n{\omega}_0t)-sin(1.5n{\omega}_0t))$$

Is this suffice as an answer, or am I missing something? My textbook is lacking examples so I just would like to know if I am doing it right. Thanks!

 

[sandy.bridge]

I also had encountered another equation deeper in the chapter that states
$$f(t)=A/2+(2A/\pi)\sum_{n=1}^{\infty}\frac{sin((2n-1)\omega{_0}t)}{2n-1}$$