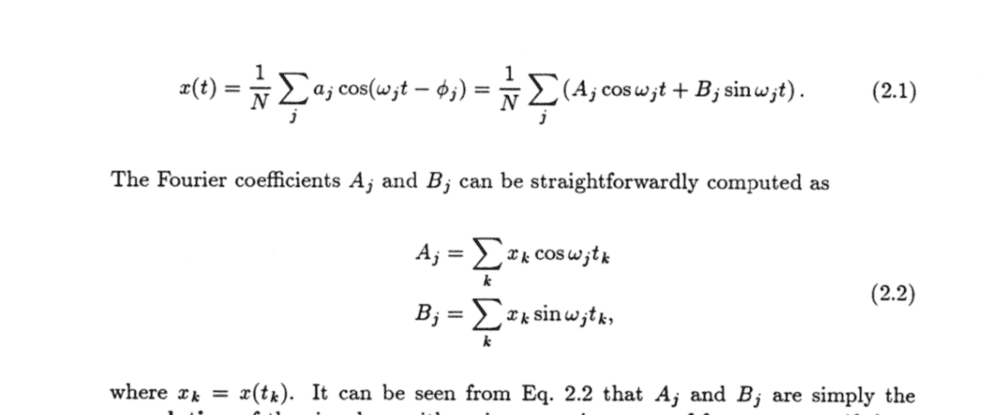SUMMARY
The discussion focuses on the derivation of Equation (2.2) related to Fourier coefficients, specifically addressing the confusion surrounding the definition of ##t_k## and the summation notation Σk. Participants clarify that the derivation involves substituting the solutions for coefficients A_j and B_j into the equation for x_k, leading to a simplification that confirms the relationship. The reference paper provided, which includes these derivations, is titled "Fourier Techniques" and can be accessed for further details.
PREREQUISITES
- Understanding of Fourier coefficients and their applications
- Familiarity with trigonometric identities and their use in summation
- Basic knowledge of mathematical notation and derivation techniques
- Access to the paper "Fourier Techniques" for reference
NEXT STEPS
- Review the derivation of Fourier coefficients in the paper "Fourier Techniques"
- Study the application of trigonometric identities in Fourier analysis
- Explore advanced topics in Fourier transforms and their implications in signal processing
- Practice derivations involving summation notation and trigonometric functions
USEFUL FOR
Students and researchers in mathematics, physics, and engineering who are working with Fourier transforms and seeking clarity on derivation techniques related to Fourier coefficients.