- #1
arcTomato
- 105
- 27
Homework Statement: I don't know how can I derivation Eq.(2.2)
Homework Equations: Fourier coefficients
Homework Statement: I don't know how can I derivation Eq.(2.2)
Homework Equations: Fourier coefficients
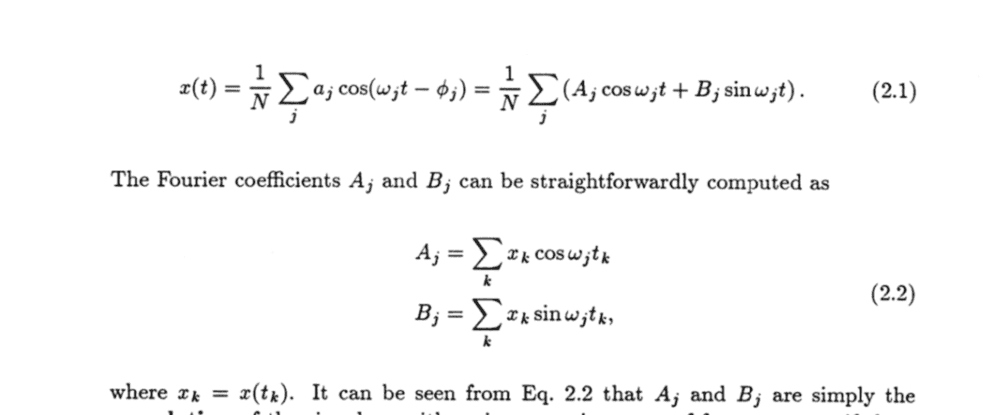
Dear all.
I don't know how can I derivation Eq.(2.2).
Where Σk is come from??
Homework Equations: Fourier coefficients
Homework Statement: I don't know how can I derivation Eq.(2.2)
Homework Equations: Fourier coefficients
Dear all.
I don't know how can I derivation Eq.(2.2).
Where Σk is come from??