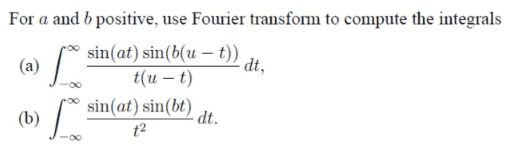Discussion Overview
The discussion revolves around solving for parameters \( a \) and \( b \) in the context of Fourier transforms, specifically involving convolutions and the application of the convolution theorem. Participants are seeking clarification on the steps necessary to compute these parameters and how to utilize software for verification.
Discussion Character
- Technical explanation
- Mathematical reasoning
- Homework-related
- Debate/contested
Main Points Raised
- Some participants suggest using the convolution theorem to evaluate the integral involving functions \( g(u) \) and \( h(u) \) defined as \( g(u) = \frac{\sin(au)}{au} \) and \( h(u) = \frac{\sin(bu)}{bu} \).
- There are multiple hints provided on how to apply the convolution theorem, including the need to find the Fourier transforms of the defined functions.
- One participant asks for clarification on the specific version of the Fourier transform being used, noting that different definitions exist which could affect the outcome.
- Another participant expresses confusion about the Fourier transform of \( \frac{\sin(bx)}{bx} \) and whether their understanding of it being \( \frac{1}{|b|} \operatorname{rect}(\frac{\omega}{2\pi b}) \) is correct.
- There is a correction regarding the definition of the sinc function, indicating that the presence of \( \pi \) must be accounted for in the calculations.
- Participants discuss the need for a table of Fourier transforms and the implications of using different conventions in software like Matlab.
Areas of Agreement / Disagreement
Participants express varying levels of understanding and agreement on the definitions and applications of the Fourier transform. There is no consensus on the correct approach to proceed with the calculations, and multiple interpretations of the definitions are present.
Contextual Notes
Limitations include the absence of a definitive version of the Fourier transform being used, potential misunderstandings regarding the sinc function, and the need for a reliable table of Fourier transforms. The discussion also highlights the dependency on the specific definitions used in software implementations.