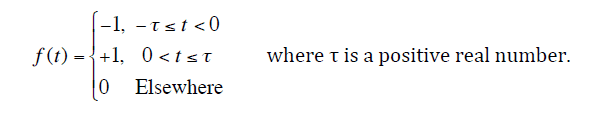SUMMARY
The discussion focuses on calculating the Fourier Transform of a piecewise function, specifically using the formula: $$ F\left[f(t)\right] = \int_{-\infty}^{\infty} dt e^{i\omega t}f(t) = \int_{-\tau}^{0} -e^{i\omega t}dt + \int_{0}^{\tau} e^{i\omega t}dt $$. The participants clarify the convention of using either \( e^{-i\omega t} \) or \( e^{i\omega t} \) depending on the context, with physics typically using \( e^{-i\omega t} \) for forward Fourier transforms. The discussion emphasizes the complexity of piecewise functions in Fourier analysis.
PREREQUISITES
- Understanding of Fourier Transform principles
- Knowledge of piecewise functions
- Familiarity with complex exponentials
- Basic integration techniques
NEXT STEPS
- Study the properties of Fourier Transforms for piecewise functions
- Learn about the differences between forward and inverse Fourier Transforms
- Explore the application of Fourier Transforms in physics
- Practice solving integrals involving complex exponentials
USEFUL FOR
Mathematicians, physicists, engineering students, and anyone interested in signal processing or Fourier analysis will benefit from this discussion.