Discussion Overview
The discussion centers around the purpose and applications of the Fourier transform, particularly in relation to Fourier series. Participants explore its significance in transforming signals from the time domain to the frequency domain, as well as its utility in various fields such as electrical engineering and signal processing.
Discussion Character
- Exploratory
- Technical explanation
- Conceptual clarification
- Debate/contested
- Mathematical reasoning
Main Points Raised
- One participant notes their familiarity with Fourier series but struggles with understanding the Fourier transform and its purpose.
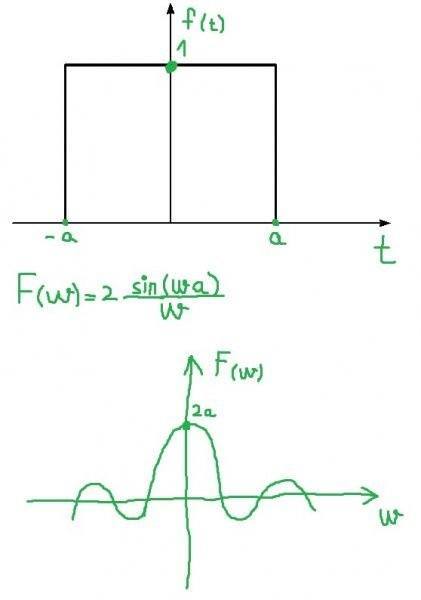
- Another participant explains that Fourier series represent a discrete case of the Fourier transform, emphasizing the periodic nature of the series and its limitations for non-repeating signals.
- A participant describes the Fourier transform as a method to represent localized signals using continuous arguments rather than discrete ones.
- Discussion includes the mathematical formulation of the Fourier transform and its relationship to the amplitudes of frequencies present in a signal.
- One participant suggests a practical application of the Fourier transform in analyzing circuit responses to nonperiodic voltage sources, indicating a method to convert time domain signals to frequency domain for analysis.
- Another participant acknowledges their lack of experience with Fourier transform applications in electricity but finds the explanation reasonable.
- A later reply highlights the importance of Fourier analysis in various fields, including digital signal processing and image analysis, and its role in simplifying calculations.
Areas of Agreement / Disagreement
Participants express various viewpoints on the applications and significance of the Fourier transform, with no consensus reached on specific applications or interpretations. Some participants agree on its utility in signal processing, while others focus on its theoretical aspects.
Contextual Notes
Participants mention specific techniques like KVL, KCL, and nodal analysis in the context of circuit analysis, but the discussion does not resolve how these techniques integrate with the Fourier transform.
Who May Find This Useful
This discussion may be useful for individuals interested in signal processing, electrical engineering, and those seeking to understand the theoretical foundations and practical applications of the Fourier transform.