Fraction of Radiation Detected

[darkchild]

Homework Statement

This is from a Physics GRE practice test:

An 8-cm-diameter by 8-cm-long NaI(Tl) detector detects gamma rays of a specific energy from a point source of radioactivity. When the source is placed just next to the detector at the center of the circular face, 50% of all emitted gamma rays at that energy are detected. If the detector is moved to 1 meter away, the fraction of detected gamma rays drops to

(A)10^{-4}
(B)2 X 10^{-4}
(C)4 X 10^{-4}
(D)8 \pi X 10^{-4}
(E)16 \pi X 10^{-4}

Homework Equations

None are given, and I don't know if there are any in particular I'm supposed to know.

The Attempt at a Solution

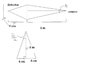
Please see the attached jpeg image for how I set my figure up. It shows the detector from the side (basically an 8cm long circular cone). I assumed that the source was still lined up with the center of the detector, i.e., just moved 1 m straight backwards. First, I decided that, when immediately adjacent to the source, the detector was privy to gamma rays emitted at any angle such that - \pi < \theta < \pi (for a total range of 180 degrees) where the angle is measured from the straight line runs from the source to the center of the detector. At 1 m distance, the magnitude of this unknown range is the variable \theta.

Using lines from the source to the edges of the detector, I constructed the triangle that is in blue. Using the right triangle,

2 \arctan (\frac{4 cm}{100 cm}) = \theta.

I expressed this as a fraction of the total angular range of emitted gamma rays using a proportion: A 180 degree range of gamma rays corresponded to 50% of the total emitted, and so:

\frac{\pi}{.5} = \frac{\theta}{x}

where x is my final answer: 0.01273 which is way off; the answer is C.

I've never even seen a problem like this before, so I'm not sure if I'm doing it correctly.

 

[zachzach]

http://grephysics.net/ans/0177/14. Most helpful website for me while studying for the GRE (along with practice tests).

 

[Rajini]

i guess you messed up..also your derivation seems to be very complex..actually it is simple..nothing to do with angle!
Do you know about the inverse law for the illumination of light/radioactive stuff..
if you apply it the answer will be 'B'?
So try with inverse square law and let me know..

 

[darkchild]

if you apply it the answer will be 'B'?
So try with inverse square law and let me know..

I have the solution set. The answer is supposed to be C.

 

[darkchild]

http://grephysics.net/ans/0177/14. Most helpful website for me while studying for the GRE (along with practice tests).

Thanks a lot. Unfortunately, there seems to be a lot of disagreement about how to find the correct answer on that post.

 

[zachzach]

Yes there is. I personally think the question is poorly written. Great site though. Good luck.

 

[Rajini]

This is my derivation.
For a point source we have the illumination formula:
\frac{\pi r^2}{4\pi l^2}
Take r=4 and l=100. [r is radius of detector and l is distance between detector and source].
Now you get 4\times 10^{-4}.
Then for 50% you need to divide the above value by 2 so the solution would be 2\times 10^{-4}.
good luck

 

[darkchild]

This is my derivation.
so the solution would be 2\times 10^{-4}.
good luck

Again, the answer is supposed to be C. I don't know whether you're saying that is a mistake/misprint, or just didn't read when I typed the answer previously.

 

[Rajini]

What is wrong in my solution?

 

[darkchild]

What is wrong in my solution?

I don't know. I don't know how to do the problem, that's why I'm trying to get help. I only have the answer letter.

 

[zachzach]

Go to the link I posted and scroll down, there are a few posts that discuss the problem. Since it is a point source it is radiating in all directions. When the detector is just next to the source it captures 50% of the photons. This corresponds to an efficiency of 100%;the detector cannot detect the photons which are going the opposite direction but detects all the photons that arrive at the detector.

 

[jrosen13]

What is wrong in my solution?

This is correct except you divided by two at the end. The question asks what fraction of the total radiation you detect. To do this absolutely correctly you are just talking about the solid angle that detector covers with the point source at the origin. At first it covers 2pi solid angle, so 2pi/4pi -> 50%

Afterwards, Rajini has shown that a great approximation for a large enough distance is to just divide from the active area of the detector the surface area of a sphere centered on the point source with radius extending to the detector. There is no reason to divide by two though, the first part was all you need to get the correct answer.

 

[Rajini]

Oh I agree guys...
Obviously i took 50% as efficiency.

 

[jrosen13]

Oh I agree guys...
Obviously i took 50% as efficiency.

Yep, you assume 100% detection efficiency in the detector (since you detect 50% right next to the source this is implied), which is basically never going to happen in real life due to charge leakage or readout noise and many other effects.