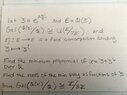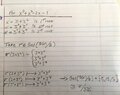Galois Groups and Minimum Polynomial

[mathjam0990]

Question

View attachment 5541

This is what I have done so far. I was wondering if anyone could verify that I found the correct minimum polynomial and roots? If I am incorrect, could someone please help me by explaining how I would find the min polynomial and roots? Thank you.

View attachment 5542View attachment 5543

 

[Deveno]

Your algebra seems to check out.

I would have simplified the working of finding the minimal polynomial of $\alpha$ like so:

$\alpha^3 = \left(\zeta + \dfrac{1}{\zeta}\right)^3 = \zeta^3 + 3\zeta + \dfrac{3}{\zeta} + \dfrac{1}{\zeta^3}$

$= \zeta^3 + \dfrac{1}{\zeta^3} + 3\alpha = \zeta^3 + \zeta^4 + 3\alpha$

and:

$\alpha^2 = \left(\zeta + \dfrac{1}{\zeta}\right)^2 = \zeta^2 + 2 + \dfrac{1}{\zeta^2} = \zeta^2 + \zeta^5 + 2$

so that:

$\alpha^3 + \alpha^2 = \zeta^3 + \zeta^4 + \zeta^2 + \zeta^5 + 3\alpha + 2$

$= \zeta + \zeta^2 + \zeta^3 + \zeta^4 + \zeta^5 + \zeta^6 + 2\alpha + 2$

$= -1 + 2\alpha + 2$, so that:

$\alpha^3 + \alpha^2 - 2\alpha - 1 = 0$.

However, this only shows that $\alpha$ is a root of the cubic $p(x) = x^3 + x^2 - 2x - 1$. To show this is the *minimal* polynomial you have two options:

1) Show it is irreducible over $\Bbb Q[x]$. I would use the rational root theorem (Gauss' lemma).

2) Show that $\sigma_6$ generates a subgroup of order 2 of $\text{Gal}(\Bbb Q(\zeta)/\Bbb Q)$, and that the fixed field of this subgroup is $\Bbb Q(\alpha)$.

You also claim without proof that the roots of $p$ are:

1) $\alpha = \zeta + \zeta^6$ (no need to prove this)
2) $\zeta^2 + \zeta^5$
3) $\zeta^3 + \zeta^4$

I would mention that this is because any automorphism of $\text{Gal}(\Bbb Q(\zeta)/\Bbb Q)$ sends a root of $p$ to another root of $p$.

Since $\Bbb Q(\alpha)$ contains all the roots of $p$, it's a normal extension (thus Galois). Clearly, its Galois group is:

$\dfrac{\text{Gal}(\Bbb Q(\zeta)/\Bbb Q)}{\text{Gal}(\Bbb Q(\zeta)/\Bbb Q(\alpha))} \cong \Bbb Z_6/\langle 3\rangle \cong \Bbb Z_3$

(recall that $3$ is the sole element of order 2 in $\Bbb Z_6$-just as complex-conjugation restricted to $\Bbb Q(\zeta)$ (the map $\sigma_6 : \zeta \mapsto \zeta^6 = \zeta^{-1} = \overline{\zeta}$) is the sole automorphism of the Galois group of $\Phi_7(x)$ of order 2).