Terry Bing
- 48
- 6
MODERATOR'S NOTE: Moved from other forum, so no template
@Chestermiller
I am still having trouble figuring out if a given process is Quasi-static or not.
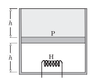
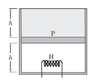
Consider the following case. The cylinder consists of an ideal gas at the bottom and a liquid of density ρ at the top separated by a piston of mass m and area A. Atmospheric pressure is p0. Again, piston and cylinder are insulating. Initially, the piston is at equilibrium. A heater is turned on in the gas. The gas will expand causing the liquid to spill out. Is this process a quasi-static adiabatic process? In this case there are no sudden changes.
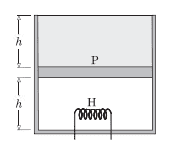
If so then the final temperature T2(when piston reaches the top) should satisfy
T2V2γ-1=T1V1γ-1.
For a monatomic gas, we have γ=5/2, which gives us T2=(0.5)3/2T1, [Since V2=2V1]
Is this correct?
@Chestermiller
I am still having trouble figuring out if a given process is Quasi-static or not.
Consider the following case. The cylinder consists of an ideal gas at the bottom and a liquid of density ρ at the top separated by a piston of mass m and area A. Atmospheric pressure is p0. Again, piston and cylinder are insulating. Initially, the piston is at equilibrium. A heater is turned on in the gas. The gas will expand causing the liquid to spill out. Is this process a quasi-static adiabatic process? In this case there are no sudden changes.
If so then the final temperature T2(when piston reaches the top) should satisfy
T2V2γ-1=T1V1γ-1.
For a monatomic gas, we have γ=5/2, which gives us T2=(0.5)3/2T1, [Since V2=2V1]
Is this correct?
Attachments
Last edited by a moderator: