Discussion Overview
The discussion centers around the concept of gauge invariance in quantum electrodynamics (QED), specifically in relation to the process $$e^+e^- \rightarrow \gamma \gamma$$ and the implications of the Ward-Takahashi identities. Participants explore the conditions under which gauge invariance holds and how it relates to current conservation and Feynman diagrams.
Discussion Character
- Technical explanation
- Debate/contested
- Mathematical reasoning
Main Points Raised
- One participant references a statement from a book regarding gauge invariance and questions how it holds under certain conditions.
- Another participant explains that the Ward-Takahashi identity arises from current conservation, which is necessary for gauge invariance.
- A participant challenges the assertion that the conditions are met, noting that the quantities involved are not zero and questioning the author's reasoning.
- It is mentioned that the Ward-Takahashi identities apply to the proper vertex function and are valid order by order in ##\hbar##, specifically for the complete set of diagrams at a given order.
- Another participant clarifies that the identities do not apply to individual diagrams but rather to the sum of diagrams relevant for the N-point function at a specific loop order.
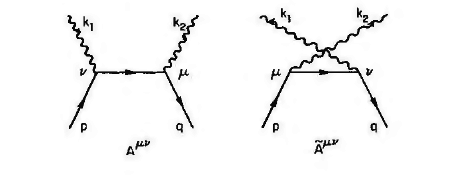
- A participant suggests that explicit calculations of the expressions for ##A^{\mu\nu}## and ##\tilde{A}^{\mu\nu}## will show that the gauge invariance conditions hold true.
- There is a question about whether the Ward-Takahashi identity applies to the amplitude rather than each individual Feynman diagram.
- A participant confirms that the identity holds for the amplitude and discusses the implications for other symmetries, such as charge conjugation symmetry, which also applies to the sum of contributions at a given loop order.
Areas of Agreement / Disagreement
Participants express differing views on the application of the Ward-Takahashi identities, particularly regarding whether they apply to individual diagrams or the sum of diagrams. The discussion remains unresolved, with multiple competing perspectives presented.
Contextual Notes
There are limitations regarding the assumptions made about the applicability of the Ward-Takahashi identities and the specific conditions under which gauge invariance is considered. The discussion also highlights the dependence on the definitions of the quantities involved and the order of perturbation theory.