KFC
- 477
- 4
Hi all,
The Gaussian wave packet is widely discussed in the text. I got the following expression for wave packet in momentum space
##\psi(p, 0) = A \exp\left[-(p-p_0)^2/ (2\sigma_p^2)\right]##
with ##A=\sqrt{2\sigma_p/\sqrt{2\pi}}##
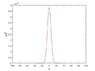
As my understanding, the corresponding wave packet in position space should be inverse Fourier transformation of ##\psi(p, 0)##. I plot the ##\psi(p, 0)## in matlab, I saw the Gaussian profile. But when I take the inverse Fourier transformation ifftshift(ifft(psi)), I saw something of the order ##10^{-6}##. I have no idea why is it.
The Gaussian wave packet is widely discussed in the text. I got the following expression for wave packet in momentum space
##\psi(p, 0) = A \exp\left[-(p-p_0)^2/ (2\sigma_p^2)\right]##
with ##A=\sqrt{2\sigma_p/\sqrt{2\pi}}##
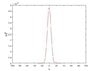
As my understanding, the corresponding wave packet in position space should be inverse Fourier transformation of ##\psi(p, 0)##. I plot the ##\psi(p, 0)## in matlab, I saw the Gaussian profile. But when I take the inverse Fourier transformation ifftshift(ifft(psi)), I saw something of the order ##10^{-6}##. I have no idea why is it.