derya
- 2
- 1
- TL;DR
- We are looking for the generic solution of this coupled system of 2nd order PDEs.
Hi! I am looking into a mechanical problem which reduces to the set of PDE's below. I would be very happy if you could help me with it.
I have the following set of second order PDE's that I want to solve. I want to solve for the generic solutions of the functions u(x,y) and v(x,y). A, B and C are constants, and (if it helps) A, B > 0.
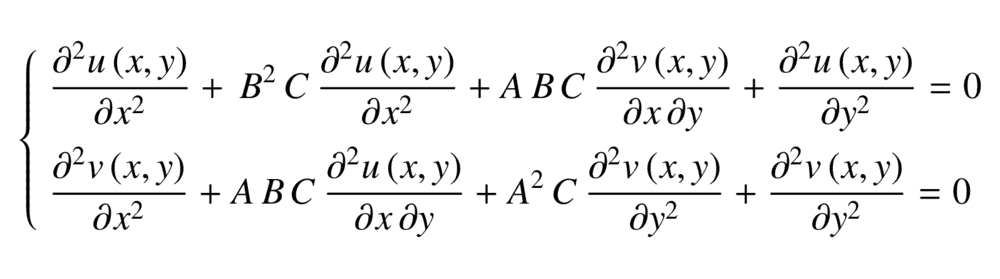
I have the following set of second order PDE's that I want to solve. I want to solve for the generic solutions of the functions u(x,y) and v(x,y). A, B and C are constants, and (if it helps) A, B > 0.