scoutfai
- 70
- 0
Geometry...is it solvable?
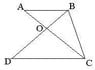
from the diagram, if AB parellel to DC, and AB = 3cm , DC = 9cm , if the triangle AOB has area 6cm^2 , then find the area of the triangle BOC.
IS this question has enough information to sovle ? if u feel yes, please show me u solution, thanks you.
from the diagram, if AB parellel to DC, and AB = 3cm , DC = 9cm , if the triangle AOB has area 6cm^2 , then find the area of the triangle BOC.
IS this question has enough information to sovle ? if u feel yes, please show me u solution, thanks you.