- #1
clope023
- 992
- 131
[SOLVED] Giant Swing, Uniform Circular Motion
The "Giant Swing" at a county fair consists of a vertical central shaft with a number of horizontal arms attached at its upper end. Each arm supports a seat suspended from a cable 5.00 long, the upper end of the cable being fastened to the arm at a point 3.00 from the central shaft.
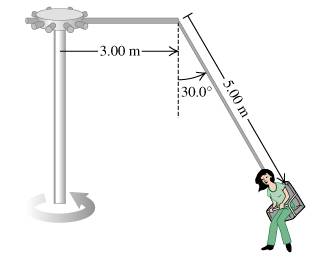
A) Find the time of one revolution of the swing if the cable supporting a seat makes an angle of with the vertical.
B) Does the angle depend on the weight of the passenger for a given rate of revolution?
R = Lsin(\theta)
v = [tex]\sqrt{gtan(\theta)R}[/tex]
T = 2[tex]\Pi[/tex]R/v
tried using L = 3+5m*sin([tex]\theta[/tex])) to get 4m
R then equals = 2m
v then equals = [tex]\sqrt{9.8*2*tan\theta}[/tex] = 11.3m/s
T then equals 2[tex]\Pi[/tex](2m)/11.3m/s = 1.1s wrong
I tried a few other combinations where I used 3+(5sintheta) as the L and got T=4.4s which was wrong as well.
I'm not sure what I'm doing wrong, I think I have the correct equations and I know I have the right angle and distances, I guess I'm just not sure how to derive the right length and and radius.
I'm also thinking that for part B the weight will determine the angle that the seat swings, but I don't want to risk losing the only chance I have on that part of the problem (masteringphysics).
any and all help is greatly appreciated.
Homework Statement
The "Giant Swing" at a county fair consists of a vertical central shaft with a number of horizontal arms attached at its upper end. Each arm supports a seat suspended from a cable 5.00 long, the upper end of the cable being fastened to the arm at a point 3.00 from the central shaft.
A) Find the time of one revolution of the swing if the cable supporting a seat makes an angle of with the vertical.
B) Does the angle depend on the weight of the passenger for a given rate of revolution?
Homework Equations
R = Lsin(\theta)
v = [tex]\sqrt{gtan(\theta)R}[/tex]
T = 2[tex]\Pi[/tex]R/v
The Attempt at a Solution
tried using L = 3+5m*sin([tex]\theta[/tex])) to get 4m
R then equals = 2m
v then equals = [tex]\sqrt{9.8*2*tan\theta}[/tex] = 11.3m/s
T then equals 2[tex]\Pi[/tex](2m)/11.3m/s = 1.1s wrong
I tried a few other combinations where I used 3+(5sintheta) as the L and got T=4.4s which was wrong as well.
I'm not sure what I'm doing wrong, I think I have the correct equations and I know I have the right angle and distances, I guess I'm just not sure how to derive the right length and and radius.
I'm also thinking that for part B the weight will determine the angle that the seat swings, but I don't want to risk losing the only chance I have on that part of the problem (masteringphysics).
any and all help is greatly appreciated.
Last edited: