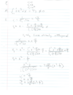SUMMARY
The discussion focuses on finding an orthonormal basis for the functions 1, x, and x² over the interval from -1 to 1 using the Gram-Schmidt process. Participants highlight the importance of expressing the final vector v₃ in closed form, specifically as v₃ = Ax² + Bx + C, rather than as a decimal. Key corrections include the unnecessary normalization of previous vectors before projection and the need to normalize v₃ after applying the Gram-Schmidt process to achieve the correct unit vector. The final expression for C should remain as C = -√10/6.
PREREQUISITES
- Understanding of the Gram-Schmidt process for orthonormalization
- Familiarity with polynomial functions and their properties
- Knowledge of vector normalization techniques
- Basic proficiency in algebraic manipulation of expressions
NEXT STEPS
- Study the Gram-Schmidt process in detail, focusing on its application to polynomial functions
- Learn about vector normalization and its significance in linear algebra
- Explore closed form expressions and their importance in mathematical solutions
- Practice problems involving orthonormal bases for various function sets
USEFUL FOR
Students and educators in mathematics, particularly those studying linear algebra and orthogonal functions, as well as anyone involved in computational mathematics or numerical analysis.