Graph Theory: (proof)conditions for Euler Circuit in Digraph

[lem0ncheezcake]

I have read in many places that one necessary condition for the existence of a Euler circuit in a directed graph is as follows.

Theorem: "A directed graph has an eulerian circuit if and only if it is connected and each vertex has the same in-degree as out-degree."

However, I don't understand why the state of being connected is a necessary condition. I thought that a Euler circuit is a closed walk where all of the edges are distinct and uses every edge in the graph exactly once. Therefore, the disconnected graph shown below should satisfy the condition of being a Euler circuit. (All the edges in the graph are used exactly once).

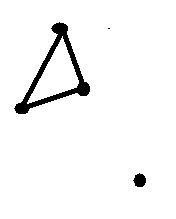
Can anyone explain what I did wrong here? Also it would be greatly appreciated if someone could give a mathematical proof to both parts of the theorem.

Thanks!

 

[Pepper Mint]

Your example graph contains a zero degreed vertex, one of whose properties your quoted theorem is still missing.

• A directed graph has an Eulerian cycle if and only if every vertex has equal in degree and out degree, and all of its vertices with nonzero degree belong to a single strongly connected component. Equivalently, a directed graph has an Eulerian cycle if and only if it can be decomposed into edge-disjoint directed cycles and all of its vertices with nonzero degree belong to a single strongly connected component.

Eulerian path and cycle or circuit.