Graphing Distance vs. Time for a Commuting Student's Forgotten Term Paper

  • Context: MHB 
  • Thread starter Thread starter mathdad
  • Start date Start date
  • Tags Tags
    Function Time
Click For Summary

Discussion Overview

The discussion revolves around graphing the distance versus time for a commuting student who forgets a term paper. Participants explore the steps to create the graph, the implications of the student's changing speed, and the interpretation of slope in the context of the problem.

Discussion Character

  • Exploratory
  • Technical explanation
  • Mathematical reasoning

Main Points Raised

  • A student drives 27 miles to college and realizes they forgot a term paper, prompting a return home.
  • Participants discuss how to represent time and distance on the graph, suggesting a linear function.
  • Some participants express uncertainty about the initial steps and the implications of the student's speed changes.
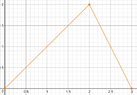
  • Questions arise about how the graph changes direction when the student returns home at a faster speed.
  • Participants analyze the meaning of points on the graph, specifically how they represent the student's distance from home over time.
  • There is a discussion about the slope of the graph, particularly how it becomes negative when the student returns home.
  • One participant attempts to calculate the slope using points on the graph, leading to confusion about the correct interpretation of steepness.
  • Another participant corrects a misunderstanding regarding the slope's sign, emphasizing that it should be negative as the distance decreases.

Areas of Agreement / Disagreement

Participants express various viewpoints on how to approach the graphing problem, with some uncertainty about the implications of speed changes and slope calculations. There is no consensus on the final representation of the graph or the interpretation of the slope.

Contextual Notes

Participants note the lack of specific information about the time spent driving before realizing the paper was forgotten, which affects the graph's accuracy. There are also unresolved questions about the calculations related to slope and the representation of distance and time.

Who May Find This Useful

This discussion may be useful for students learning about graphing functions, particularly in the context of real-world scenarios involving distance and time. It may also benefit those exploring the concepts of slope and speed in mathematical contexts.

mathdad
Messages
1,280
Reaction score
0
A student who commutes 27 miles to attend college remembers, after driving a few minutes, that a term paper that is due has been forgotten. Driving faster than usual, the student returns home, picks up the paper, and once again starts toward school. Sketch a possible graph of the student's distance from home as a function of time. What are the steps to answer this question?
 
Mathematics news on Phys.org
What have you got so far?
 
MarkFL said:
What have you got so far?

Mark,

I am on the 7 train in Queens, NYC heading back home to the Bronx. When I get home, I will post my understanding of this question, which will be wrong for sure. In fact, my work shown will not make sense and may cause some of you to ask: WHY DOESN'T THIS PRECALCULUS GUY UNDERSTAND WHAT TO DO AS A FIRST COUPLE OF STEPS?
 
RTCNTC said:
WHY DOESN'T THIS PRECALCULUS GUY UNDERSTAND WHAT TO DO AS A FIRST COUPLE OF STEPS?

No such thoughts will (or should) ever be conceived by a good teacher (as are those members here!). Any of your thoughts and working help others in identifying your particular misunderstanding. And if that means making several posts, progressively stepping through the problem, so be it.
 
Let the x-axis = time of travel in hours

Let the y-axis = miles traveled

I think we are talking about a straight line or linear function graph.

The question does not state the amount of minutes the student drove before realizing that he forgot his term paper nor does it mentions the length he drove.

On the graph, A is the time in minutes he drove and B the length. See picture. Is this correct?

View attachment 7868
 

Attachments

  • sDraw_2018-02-26_02-44-52.png
    sDraw_2018-02-26_02-44-52.png
    8.8 KB · Views: 130
Looks good so far...now what's going to happen when the student heads back home at a faster speed?
 
MarkFL said:
Looks good so far...now what's going to happen when the student heads back home at a faster speed?

The graph changes direction? Must I draw another arrow pointing downward?
 
RTCNTC said:
The graph changes direction? Must I draw another arrow pointing downward?

Suppose the vertical axis is $d$ and the horizontal $t$, to represent distance and time, respectively. What does a point $(t,d)$ represent?
 
MarkFL said:
Suppose the vertical axis is $d$ and the horizontal $t$, to represent distance and time, respectively. What does a point $(t,d)$ represent?

The point (t, d) represents the student's distance from home.
 
  • #10
RTCNTC said:
The point (t, d) represents the student's distance from home.

The vertical distance of the point above the $t$-axis represents this distance, while the horizontal distance of the point to the $d$-axis to its left represents the time.

When the student returns toward home, what should be happening to the coordinates of the points on the graph?
 
  • #11
MarkFL said:
The vertical distance of the point above the $t$-axis represents this distance, while the horizontal distance of the point to the $d$-axis to its left represents the time.

When the student returns toward home, what should be happening to the coordinates of the points on the graph?

The coordinates of the point (t, d) should be increasing or decreasing.
 
  • #12
RTCNTC said:
The coordinates of the point (t, d) should be increasing or decreasing.

As the student returns home, time is increasing (moving forward), but the distance from home is decreasing and so the slope of the graph will be negative. How will the magnitude of the slope compare to when the student was moving away from hom before turning back?
 
  • #13
MarkFL said:
As the student returns home, time is increasing (moving forward), but the distance from home is decreasing and so the slope of the graph will be negative. How will the magnitude of the slope compare to when the student was moving away from hom before turning back?

I do not understand? Magnitude of the slope?
 
  • #14
RTCNTC said:
I do not understand? Magnitude of the slope?

How steep will it be, in comparison to the first part of the trip?
 
  • #15
By "steep" you are talking about slope but I don't get it.

Origin = (0,0)

Our point is (t, d)

Can you steepness be found using these 2 points?

m = (t - 0)/(d - 0)

m = t/d

Does the value of m here satisfy the "steep" part of your question?
 
  • #16
RTCNTC said:
By "steep" you are talking about slope but I don't get it.

Origin = (0,0)

Our point is (t, d)

Can you steepness be found using these 2 points?

m = (t - 0)/(d - 0)

m = t/d

Does the value of m here satisfy the "steep" part of your question?

Excellent! Now, suppose the student travels back home twice as fast as he left...what will the slope of the second part of the trip be?
 
  • #17
The slope of the second part of his trip is 2(t/d).
 
  • #18
RTCNTC said:
The slope of the second part of his trip is 2(t/d).

Let's check:

$$m=\frac{\Delta d}{\Delta t}=\frac{0-d}{\frac{3}{2}t-t}=-\frac{d}{\frac{1}{2}t}=-2\frac{d}{t}$$

I didn't notice earlier that you mixed up $d$ and $t$.
 
  • #19
The answer is -2(d/t) not 2(d/t). Why a negative slope?
 
  • #20
RTCNTC said:
The answer is -2(d/t) not 2(d/t). Why a negative slope?

Shouldn't we expect a negative slope since the $d$ coordinate will be moving towards the $t$-axis from some positive value, towards where $d=0$?
 
  • #21
And so, the final answer to this question is?
 
  • #22

Attachments

  • rtc_dt.png
    rtc_dt.png
    4.5 KB · Views: 98
  • #23
MarkFL said:
It could look something like:

You are truly gifted. Thanks.
 

Similar threads

High School Graphing trip efficiency - distance over time
  • · Replies 14 ·
Replies
14
Views
3K
MHB Solving Inequalities and Quadratic story problems
  • · Replies 2 ·
Replies
2
Views
2K
Programs Major Guidance: A problematic situation
  • · Replies 2 ·
Replies
2
Views
4K
Graduate Time and Indeterminacy vs. Continuity
  • · Replies 14 ·
Replies
14
Views
6K
At a crossroads (drop out? chase a dream? time out?)
  • · Replies 13 ·
Replies
13
Views
5K
Mathematica This Week's Finds in Mathematical Physics (Week 259)
  • · Replies 1 ·
Replies
1
Views
3K
Fork in the road, each path leads to possibly more disappointment.
  • · Replies 42 ·
2
Replies
42
Views
8K
Mathematica This Week's Finds in Mathematical Physics (Week 257)
  • · Replies 5 ·
Replies
5
Views
5K
Graduate Big Bang Big Schmang, astronomical redshift is an artifact of distance
  • · Replies 1 ·
Replies
1
Views
3K
Mathematica This Week's Finds in Mathematical Physics (Week 264)
  • · Replies 6 ·
Replies
6
Views
5K