fzero said:
You should probably just look at the computation leading up to (44.18) in
http://www.physics.ucsb.edu/~mark/ms-qft-DRAFT.pdf What I should have realized sooner is that multiplying differentials almost never leads to the correct measure. What is true is that you could compute the measure from the volume form if you're careful. But it's usually faster to use the Jacobian.
So what are our J_{i_1j_1} in this case?
fzero said:
The diagrams corresponding to the expansion of what's usually called the generating function (usually written as W[J]) are connected and include propagators on the external legs. What's usually called the effective action (\Gamma[\phi]) involves the one-particle irreducible diagrams with no propagators on the external legs.
Yes, I have these same definitions. But this doesn't explain why we consider 1PI diagrams? Is it because they don't have propagators on the external legs and are therefore simpler to deal with?
fzero said:
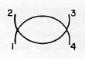
The diagram I'm talking about is
Ok so given this graph, if we put k as the loop momenta then the Euclidean space Feynman rules tell us that we get
\int \frac{d^dk}{(2 \pi)^d} \frac{1}{k^2+m^2} \frac{1}{(p-k)^2+m^2} \rightarrow \int \frac{d^dk}{(2 \pi)^d} \frac{1}{k^4}
If we regularise by imposing a high momentum UV cutoff k \leq \Lambda
then we obtain the result \tilde \log{\Lambda} as on p324 P&S.
Is this correct?
Also, when we compute these loop integrals, what exactly are we computing? He just draws a diagram and then puts something like ~ log (k) next to it but doesn't actually say WHAT IS ~log(k). It's not a green's function or anything like that. What actually is it?
fzero said:
All we've done is applied the \phi\rightarrow -\phi symmetry to the correlator. There's no need to evaluate it since we've shown that it must be zero.
Do you just mean that you took \langle \phi(x_1) \phi(x_2) \phi(x_3) \rangle and made the transformation \phi \rightarrow - \phi which gives 3 minus signs (one for each \phi) and since (-1)^3=-1 we get an overall minus sign that we can pull out showing that the 3 point green's function is equal to minus itself and therefore must vanish?
fzero said:
You could compute a residue or principal value, but the factorial does not extend to the whole plane. It extends to everywhere that it doesn't have a pole, which is the plane minus the nonpositive integers.
Ok. So you're telling me that \Gamma is defined everywhere except 0,-1,-2,-3,...?
But we just showed a few posts ago that \Gamma(0)=1 to be consistent with 0!=1
So if you were asked to find (-1.5)!, could you just compute \Gamma(-0.5) using its integral definition as \Gamma(\alpha) = \int_0^\int x^{\alpha-1}e^{-x}dx?
Lastly, my notes discuss three methods of regularisation: (i) UV cut-off which I think I understand (assuming you agree with my calculation of \log(\Lambda) above.
(ii) Using a spacetime lattice (although this doesn't seem very important as he just mentions it in passing.
(iii) Dimensional Regularisation. This seems like the most important. He just says though:
The superficial degree opf divergence is given by D=(d-4)L + \displaystyle\sum_n (n-4) V_n - E + 4 which depends on the dimension d.
Usually this is just defined for d \in \mathbb{Z}^+ but we can regulate by analytic continuation to d \in \mathbb{C}.
He has included an example afterwords and I can follow the maths in it but I don't really understand what we are doing. How do we analytically continue to complex d and what's the point of doing so?
Thanks very much!