SpectraPhy09
- 23
- 3
- Homework Statement
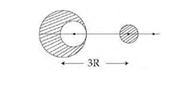
- From a sphere of mass M and radius R, a smaller sphere of radius R/2 is carved out such that a cavity made in the original sphere is between its centre and periphery (Plz check the image I have attached). For this configuration in the figure where distance between the centre and the original sphere and the removed sphere is 3R, the gravitational force between the two sphere is?
- Relevant Equations
- F = GM1M2/r²
Density of the Sphere = 3M/4πR³
Mass of carved out sphere
= density × 4π/3 × R³/8
= M/8
The position of center of mass of The Sphere

{M(0) - M/8(R/2)}/M-M/8
-R/14
So total distance between centers of the two bodies is R/14 + 3R = 43R/14
So now I found force between the Mass 7M/8 (left out mass) and M/8
F = (G 7M/8 × M/8)/ (43R/14)²
F = 343GM²/2958R²
But this ans is given incorrect in my textbook
Is my approach wrong, or did I did something wrong?
Also is there any other method to solve this question?
Mass of carved out sphere
= density × 4π/3 × R³/8
= M/8
The position of center of mass of The Sphere
{M(0) - M/8(R/2)}/M-M/8
-R/14
So total distance between centers of the two bodies is R/14 + 3R = 43R/14
So now I found force between the Mass 7M/8 (left out mass) and M/8
F = (G 7M/8 × M/8)/ (43R/14)²
F = 343GM²/2958R²
But this ans is given incorrect in my textbook
Is my approach wrong, or did I did something wrong?
Also is there any other method to solve this question?