Gravitational Forces between two masses

[SpectraPhy09]

Homework Statement

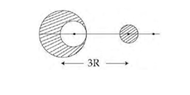
From a sphere of mass M and radius R, a smaller sphere of radius R/2 is carved out such that a cavity made in the original sphere is between its centre and periphery (Plz check the image I have attached). For this configuration in the figure where distance between the centre and the original sphere and the removed sphere is 3R, the gravitational force between the two sphere is?

Relevant Equations

F = GM1M2/r²

Density of the Sphere = 3M/4πR³
Mass of carved out sphere
= density × 4π/3 × R³/8
= M/8
The position of center of mass of The Sphere

{M(0) - M/8(R/2)}/M-M/8
-R/14

So total distance between centers of the two bodies is R/14 + 3R = 43R/14

So now I found force between the Mass 7M/8 (left out mass) and M/8
F = (G 7M/8 × M/8)/ (43R/14)²
F = 343GM²/2958R²
But this ans is given incorrect in my textbook
Is my approach wrong, or did I did something wrong?
Also is there any other method to solve this question?

 

[jbriggs444]

The

The position of center of mass of The Sphere

The problem is that you no longer have a sphere.

Newton's universal law of gravitation ($F=\frac{Gm_1m_2}{r^2}$) works for point objects and for spherically symmetric objects. It does not work for oddly shaped objects such as spheres with holes carved out. [Newton's Shell Theorem is how you prove that spheres work]

There is a trick that you are expected to use here. Consider the original sphere with a smaller sphere of negative density super-imposed within it. This is the same thing as a hole, but is easier to calculate with.

Note that I have not checked your math for errors. Only your approach.

 

[SpectraPhy09]

Consider the original sphere with a smaller sphere of negative density super-imposed within it

But how can there be a negative Mass density?
This same approach is there in my textbook also But I didn't get it

 

[jbriggs444]

But how can there be a negative Mass density?
This same approach is there in my textbook also But I didn't get it

The gravitational effect of a sphere with a hole is the same as the gravitational effect of the whole sphere minus the effect of the material that once filled the hole, do you agree?

If so, work the problem that way.

The math does not care whether you subtract positive mass or add negative mass.

 

[kuruman]

Think superposition. If the sphere were solid and you calculated the force between it and the smaller sphere, that would be too much. You have to subtract something. See figure below.

 

[PeroK]

But how can there be a negative Mass density?
This same approach is there in my textbook also But I didn't get it

I don't get it either! Instead:

Gravity of big sphere = Gravity of big sphere with little sphere missing + Gravity of little sphere

Hence:

Gravity of big sphere with little sphere missing = Gravity of big sphere - Gravity of little sphere

No need for negative mass density!