Greatest Common Divisor Theorems definition clarification.

[knockout_artist]

Hi,

I read definition of GCD theorem, from book and from mathWorld website.

"
There are two different statements, each separately known as the greatest common divisor theorem.
This does not make sanse
1. Given positive integers

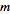and

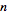, it is possible to choose integers

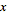and

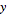such that

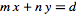, where

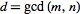is the greatest common divisor of

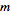and

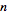(Eynden 2001).
This make sense

2. If

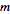and

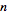are relatively prime positive integers, then there exist positive integers

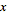and

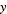such that

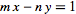(Johnson 1965).
"
======================================
if I take 2nd definition from above

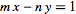
and take
m=12
n=7
then divisors:

12X1,6x2,4x3
7x1
gdc=1

and according to second definition.
x=3
y=5
xm - ny = 1
(12x3 ) - (7x5) = 1
36 -35 = 1
it make sense.
========================================
but 1st definition says

,
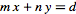we take again
m=12 and
n=7

no matter what values of 'x' and 'y' we pick, we can not make d smaller so it can become '1'.
Unless we select negative x and y.

 

[fresh_42]

no matter what values of 'x' and 'y' we pick, we can not make d smaller so it can become '1'.
Unless we select negative x and y.

So? The sign doesn't play any role in here, since $\pm 1$ are both unities (inverible elements). The emphasis on positive integers in definition 2 isn't really necessary here. Maybe Johnson needed it for further proofs in his context. But as the entire concept deals with the nature of integers, there is simply no meaning in dividing them into positive and negative numbers.